Acronym	giddic
Name	great distetracontoctachoron
Cross sections	©
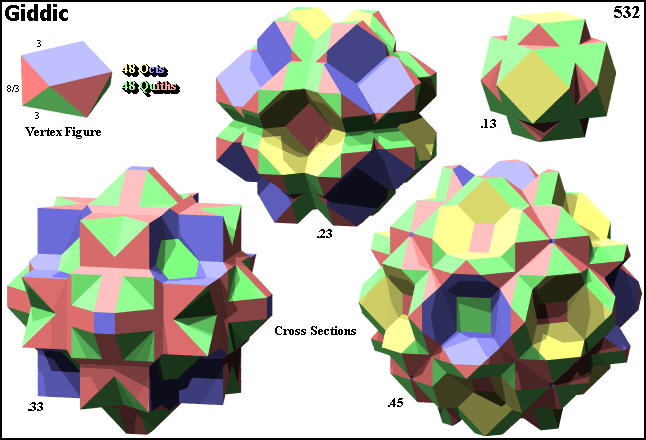Circumradius	sqrt[2-sqrt(2)] = 0.765367
Coordinates	(0, 0, sqrt(2), 2-sqrt(2))/2           & all permutations, all changes of sign (1, 1, sqrt(2)-1, sqrt(2)-1)/2       & all permutations, all changes of sign (vertex inscribed qrit)
General of army	spic
Colonel of regiment	(is itself locally convex – uniform polychoral members: by cells: gocco groh oct querco quith trip gamfaddic 48 0 48 0 0 0 girc 0 48 0 0 0 0 giddic 0 0 48 0 48 0 irnpac 0 0 48 24 0 96 quippic 0 0 48 0 0 192 & others)
Face vector	144, 576, 528, 96
Confer	general polytopal classes: Wythoffian polychora
External links

As abstract polytope giddic is isomorphic to siddic, thereby replacing octagrams by octagons, and thus quith by tic.

Incidence matrix according to Dynkin symbol

     4/3     
    x---x    
  3 |   | 3  
    o---o    
      4      

x3o4o3x4/3*a

. . . .      | 144 |   4   4 |   4   8   4 |  1  4  4  1
-------------+-----+---------+-------------+------------
x . . .      |   2 | 288   * |   2   2   0 |  1  2  1  0
. . . x      |   2 |   * 288 |   0   2   2 |  0  1  2  1
-------------+-----+---------+-------------+------------
x3o . .      |   3 |   3   0 | 192   *   * |  1  1  0  0
x . . x4/3*a |   8 |   4   4 |   * 144   * |  0  1  1  0
. . o3x      |   3 |   0   3 |   *   * 192 |  0  0  1  1
-------------+-----+---------+-------------+------------
x3o4o .      ♦   6 |  12   0 |   8   0   0 | 24  *  *  *
x3o . x4/3*a ♦  24 |  24  12 |   8   6   0 |  * 24  *  *
x . o3x4/3*a ♦  24 |  12  24 |   0   6   8 |  *  * 24  *
. o4o3x      ♦   6 |   0  12 |   0   0   8 |  *  *  * 24

or
. . . .         | 144 |   8 |   8   8 |  2  8
----------------+-----+-----+---------+------
x . . .       & |   2 | 576 |   2   2 |  1  3
----------------+-----+-----+---------+------
x3o . .       & |   3 |   3 | 384   * |  1  1
x . . x4/3*a    |   8 |   8 |   * 144 |  0  2
----------------+-----+-----+---------+------
x3o4o .       & ♦   6 |  12 |   8   0 | 48  *
x3o . x4/3*a  & ♦  24 |  36 |   8   6 |  * 48

     4/3     
    x---x    
  3 |   | 3/2
    o---o    
     4/3     

x3o4/3o3/2x4/3*a

. .   .   .      | 144 |   4   4 |   4   8   4 |  1  4  4  1
-----------------+-----+---------+-------------+------------
x .   .   .      |   2 | 288   * |   2   2   0 |  1  2  1  0
. .   .   x      |   2 |   * 288 |   0   2   2 |  0  1  2  1
-----------------+-----+---------+-------------+------------
x3o   .   .      |   3 |   3   0 | 192   *   * |  1  1  0  0
x .   .   x4/3*a |   8 |   4   4 |   * 144   * |  0  1  1  0
. .   o3/2x      |   3 |   0   3 |   *   * 192 |  0  0  1  1
-----------------+-----+---------+-------------+------------
x3o4/3o   .      ♦   6 |  12   0 |   8   0   0 | 24  *  *  *
x3o   .   x4/3*a ♦  24 |  24  12 |   8   6   0 |  * 24  *  *
x .   o3/2x4/3*a ♦  24 |  12  24 |   0   6   8 |  *  * 24  *
. o4/3o3/2x      ♦   6 |   0  12 |   0   0   8 |  *  *  * 24

     4/3     
    x---x    
3/2 |   | 3/2
    o---o    
      4      

x3/2o4o3/2x4/3*a

.   . .   .      | 144 |   4   4 |   4   8   4 |  1  4  4  1
-----------------+-----+---------+-------------+------------
x   . .   .      |   2 | 288   * |   2   2   0 |  1  2  1  0
.   . .   x      |   2 |   * 288 |   0   2   2 |  0  1  2  1
-----------------+-----+---------+-------------+------------
x3/2o .   .      |   3 |   3   0 | 192   *   * |  1  1  0  0
x   . .   x4/3*a |   8 |   4   4 |   * 144   * |  0  1  1  0
.   . o3/2x      |   3 |   0   3 |   *   * 192 |  0  0  1  1
-----------------+-----+---------+-------------+------------
x3/2o4o   .      ♦   6 |  12   0 |   8   0   0 | 24  *  *  *
x3/2o .   x4/3*a ♦  24 |  24  12 |   8   6   0 |  * 24  *  *
x   . o3/2x4/3*a ♦  24 |  12  24 |   0   6   8 |  *  * 24  *
.   o4o3/2x      ♦   6 |   0  12 |   0   0   8 |  *  *  * 24

or
.   . .   .         | 144 |   8 |   8   8 |  2  8
--------------------+-----+-----+---------+------
x   . .   .       & |   2 | 576 |   2   2 |  1  3
--------------------+-----+-----+---------+------
x3/2o .   .       & |   3 |   3 | 384   * |  1  1
x   . .   x4/3*a    |   8 |   8 |   * 144 |  0  2
--------------------+-----+-----+---------+------
x3/2o4o   .       & ♦   6 |  12 |   8   0 | 48  *
x3/2o .   x4/3*a  & ♦  24 |  36 |   8   6 |  * 48