|
Acronym
|
...
|
|
Name
|
cell of gap dual,
adjacent bikis doe
|
|
|
 © ©
|
|
Vertex figure
|
[53], [52,K], [5,K2], [5,K,T], [k2,t2]
|
Lace city
in approx. ASCII-art
|
o o
f f
o o
x x
v
|
f
v v
f
x x
o o
|
Dihedral angles
(at margins)
|
- at singular long edge: arccos(1/sqrt(5)) = 63.434949°
- at all other edges: arccos(-1/sqrt(5)) = 116.565051°
|
|
Face vector
|
14, 22, 10
|
|
Confer
|
- uniform relative:
-
doe
gad
|
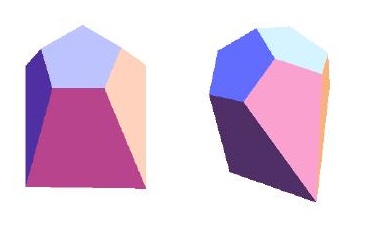
This polyhedron can also be obtained as a stellation of doe by blending at
2 neighbouring pentagons with tall pyramids, which are the tips of sissid and then inserting inbetween a wedge type simplex,
as is used for gad.
The faces are regular pentagons of side v = (sqrt(5)-1)/2 = 0.618034; kites {(k,K,K,K)} with corner angle k = 36° and K = 108°,
where side KK has size v again, diagonal KK has size x = 1, side kK has size f = (1+sqrt(5))/2 = 1.618034, and the diagonal kK has
size sqrt[(5+sqrt(5))/2] = 1.902113; and trapzia {(t,t,T,T)} with corner angle t = 72° and T = 108°, where the side TT has size v again,
while the other sides tT and tt have both size f again.
Incidence matrix according to Dynkin symbol
ofoxv fvfxo&#(f,v)t → height(1,2) = (3+sqrt(5))/4 = 1.309017
height(2,3) = height(4,5) = (sqrt(5)-1)/4 = 0.309017
height(3,4) = (3-sqrt(5))/4 = 0.190983
o.... o.... | 2 * * * * | 1 2 1 0 0 0 0 0 | 2 2 0 0 [k2,t2]
.o... .o... | * 4 * * * | 0 1 0 1 1 0 0 0 | 1 1 1 0 [5,K,T]
..o.. ..o.. | * * 2 * * | 0 0 1 0 0 2 0 0 | 0 2 0 1 [5,K2]
...o. ...o. | * * * 4 * | 0 0 0 0 1 1 1 0 | 0 1 1 1 [52,K]
....o ....o | * * * * 2 | 0 0 0 0 0 0 2 1 | 0 0 1 2 [53]
--------------------+-----------+-----------------+--------
..... f.... | 2 0 0 0 0 | 1 * * * * * * * | 2 0 0 0
oo... oo...&#f | 1 1 0 0 0 | * 4 * * * * * * | 1 1 0 0
o.o.. o.o..&#f | 1 0 1 0 0 | * * 2 * * * * * | 0 2 0 0
..... .v... | 0 2 0 0 0 | * * * 2 * * * * | 1 0 1 0
.o.o. .o.o.&#v | 0 1 0 1 0 | * * * * 4 * * * | 0 1 1 0
..oo. ..oo.&#v | 0 0 1 1 0 | * * * * * 4 * * | 0 1 0 1
...oo ...oo&#v | 0 0 0 1 1 | * * * * * * 4 * | 0 0 1 1
....v ..... | 0 0 0 0 2 | * * * * * * * 1 | 0 0 0 2
--------------------+-----------+-----------------+--------
..... fv...&#f | 2 2 0 0 0 | 1 2 0 1 0 0 0 0 | 2 * * * {(t,t,T,T)}
oooo. oooo.&#r(f,v) | 1 1 1 1 0 | 0 1 1 0 1 1 0 0 | * 4 * * {(k,K,K,K)}, cycle (a,b,d,c)
..... .v.xo&#vt | 0 2 0 2 1 | 0 0 0 1 2 0 2 0 | * * 2 * {5}
..oxv .....&#vt | 0 0 1 2 2 | 0 0 0 0 0 2 2 1 | * * * 2 {5}
©