- related hyperbolic polytopes:
- pex-o3o4o3*a pac-o3o4x3*a o3o4x3*a
- general polytopal classes:
- partial Stott expansions
| Acronym | ... |
| Name | hyperbolic [(33,4)4] tiling |
|
| |
| Vertex figure | [(33,4)4] |
| Confer |
|
Although this tiling is uniform, it neither has a triangular fundamental domain, nor directly relates to those tilings with Coxeter domains.
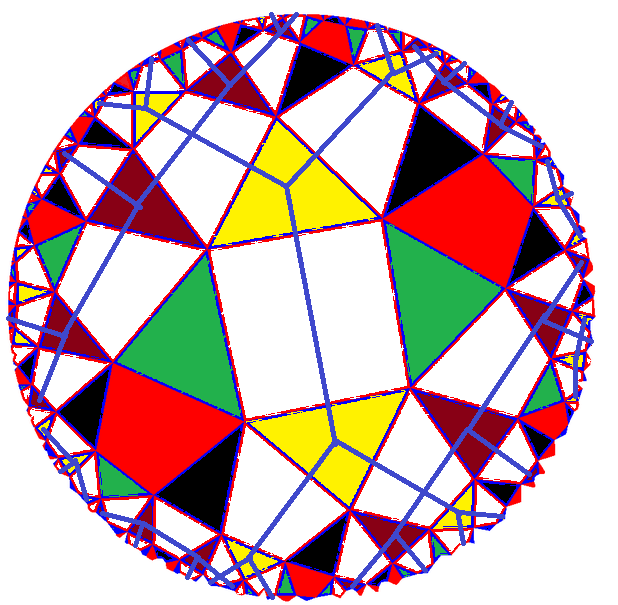
This tiling could be obtained by a 2 step partial Stott contraction from o3o4x3*a: first color the triangles of that tiling in 4 colors, say yellow, brown, black, and green. Then apply a tripesic contraction, which would contract all yellow triangles into just vertices: this would result in pac-o3o4x3*a. Then apply a second such contraction onto that, reducing the brown triangles into points too. This would be the tiling under consideration. – One even could apply this again with respect to the black triangles. Then only the green triangles would be left, providing pex-o3o4o3*a. (A fourth application then clearly would reduce the complete tiling into a single point.)
(N → ∞)
N | 4 4 4 4 | 6 6 4 [((3^3),4)^4]
--+-------------+--------
2 | 2N * * * | 2 0 0 s:s
2 | * 2N * * | 0 2 0 g:g
2 | * * 2N * | 1 0 1 s:r
2 | * * * 2N | 0 1 1 g:r
--+-------------+--------
3 | 2 0 1 0 | 2N * * s {3}
3 | 0 2 0 1 | * 2N * g {3}
4 | 0 0 2 2 | * * N r {4}
pabex-o3o4o3*a (y-triangle → pt & b-triangle → pt) (N → ∞)
N | 2 2 2 2 4 4 | 6 6 4 [((3^3),4)^4]
--+---------------+--------
2 | N * * * * * | 2 0 0 s:y
2 | * N * * * * | 2 0 0 s:b
2 | * * N * * * | 0 2 0 g:y
2 | * * * N * * | 0 2 0 g:b
2 | * * * * 2N * | 1 0 1 s:r
2 | * * * * * 2N | 0 1 1 g:r
--+---------------+--------
3 | 1 1 0 0 1 0 | 2N * * s {3}
3 | 0 0 1 1 0 1 | * 2N * g {3}
4 | 0 0 0 0 2 2 | * * N r {4}
© 2004-2025 | top of page |