⭳




the corresponding VRML preview in this canvas
= oct
= thah
= squippy
= bobipyr
| Site Map | Polytopes | Dynkin Diagrams | Vertex Figures, etc. | Incidence Matrices | Index |
Possible facets here are the 8 triangles of the comodore itself and the 3 diametral squares. The general naming code here is accordingly oct-#{3}-#{4}. This gives rise for exactly 4 edge-facetings, without any further restriction. Only 3 of those have n-gonal axial rotation symmetries with n > 2. In fact, just 1 has full octahedral symmetry, 1 has tetrahedral symmetry, and 1 has 4-fold pyramidal symmetry. The fourth possible edge-faceting has 2-fold briquet symmetry only.
|

|

|

|

| ||
|
clicking the triple-pictures of the table provides the corresponding VRML preview in this canvas |
oct-8-0 = oct |
oct-4-3 = thah |
oct-4-1 = squippy |
oct-4-2 = bobipyr | ||
| octahedral | tetrahedral | 4-fold pyramidal | 2-fold briquet | |||
Possible facets here are the 8 triangles and 6 squares of the comodore itself together with the 4 diametral hexagons. The general naming code here is accordingly co-#{3}-#{4}-#{6}. This gives rise for exactly 7 edge-facetings, without any further restriction. Only 5 of those have n-gonal axial rotation symmetries with n > 2. In fact, 3 have full octahedral symmetry, and 2 have 3-fold pyramidal symmetry. The other possible edge-facetings have 2-fold briquet symmetry only.
|

|

|

|
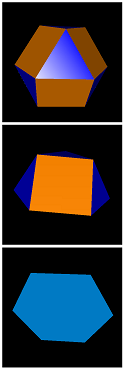
|

|

|

| ||
|
clicking the triple-pictures of the table provides the corresponding VRML preview in this canvas |
co-8-6-0 = co |
co-8-0-4 = oho |
co-0-6-4 = cho |
co-4-3-1 = tricu |
co-4-3-3 = gripper |
co-4-4-2 = bocuco |
co-4-2-2 = ebot | ||
| octahedral | 3-fold pyramidal | 2-fold briquet | |||||||
© 2004-2025 | top of page |