Welcome to the Home of Polytiles!
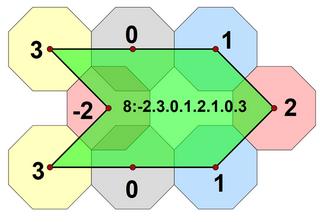
An example octatile
8:-2.3.0.1.2.1.0.3,
is an octagon, with 1 concave angle and 2 straight angles. |
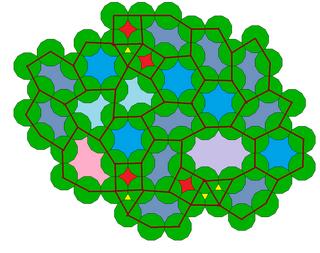
A partial
tiling of regular dodecagon structures dodecatiles in the gaps, using
the center of the dodecagons as vertices, and edge-to-edge pairs of dodecagons
define edges. |
-
What is a polytile?
-
A polytile is an
equilateral
polygon with vertex angles limited to integer multiples of 360/p
degrees for p as an even positive integer. A tetratile (4-tile)
has vertex angles as multiples of 90°. A hexatile (6-tile) has
angles multiples of 60°. An octatile (8-tile) has angles multiples
of 45°. A decatile (10-tile) has angles multiples of 36°.
A dodecatile (12-tile) has angles multiples of 30°. And so on.
-
How are polytiles defines?
-
Polytile notation is used to define a polytile.
It has a structure:
p:a1.a2...am^n, repeating the sequence
of m angles n times. Each ai represents a
turn angle scaled
as steps on a regular p-gon, best limited beween
|ai|<p/2. A zero turn angle defines 2 colinear edges,
positive turn angles turn counter-clockwise, and negative turn angles turn
clockwise. For example, a
square is tetratile,
4:1.1.1.1
or 4:1^4, as well as
octatile 8:2^4 and dodecatile
12:3^4. If the p: is
not given, is computed as the sum of all the angles,
p=nΣai.
-
What can I do with polytiles?
-
Polytiles can be used as
prototiles of
tessellations
of edge-to-edge polygons. Polytiles can also define star polygons, polygons
whose turn angles sum to multiples of 360°.
-
How can I use them?
-
The javascript
applications below (will) allow users to test polytiles by inputing polytile
notation, and building tilings with them.
Papers
-
[PDF 4.2M] Polytiles: Equilateral
and Equiangular Polygons (part 1a) -
[abstract]
Published
Oct 15, 2021 at
eJMT
-
[PDF 6.9M] Convex Polytiles
Enumerations (part 1b) Zonogons, Progons, and Exotics -
[abstract]
Published
Feb 15, 2023 at
eJMT
-
[PDF 3.4M] Four Polytope Products:
Join, Fusil, Prism, and Meet -
[abstract]
[published]
Feb 15, 2024 at
eJMT
Javascript applications
Informational Pages (in progress)
© 2020-2021 Created by Tom Ruen
 (Reset 7/14/21) (Reset 7/14/21)
|
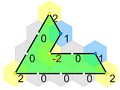 Polytiles
Polytiles
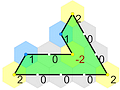
 Polytiles
Polytiles
