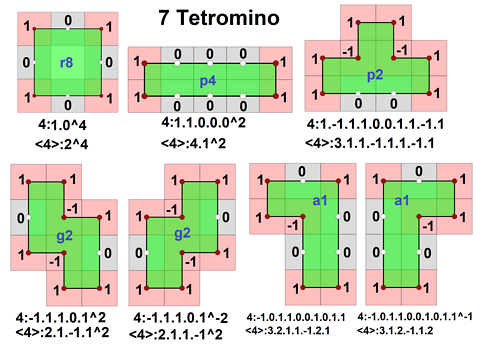
 Tetrominos |
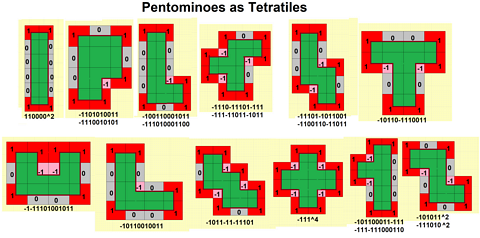 Pentominos |
Polyominos
Polyominos are tiles created as the union of edge-to-edge connected square. They are classified by the number of squares monomino=1, domino=2, tromino=3, tetromino=4, pentomino=5, hexomino=6, heptomino=7, octomino=8, nonomino=9, decomino=10. They can be enumerated with different counts, allowing or disallowing rotations, allowing or disallowing reflections, and allowing or disallowing holes.
There's only one monomino, a square, and one domino, a 2x1 rectangle with 2 orientations. There are 2 triminos, with 6 orientations. There are 3 tetrominos, 5 tetrominos with chiral pairs and 19 with unique orientations. As tetratiles they are: 4:10^4, 4:11000^2, 4:-11101^2, 4:1-1110011-11, 4:-1011001011.
The game Tetris has falling Tetrominos which have to fill a solid level to clear.
There are 12 pentominos, 18 with chiral pairs.
Polyominos can make puzzles, how to fill (dissect) a given permeter of squares with a given set of polyominos.
Tetratile notation can express all of them in either equilateral or equiangular notation. Equilateral notation starts with 4: and sequences angles -1,0,1. Equiangular notation starts with <4>: and sequences integer edge lengths, with a negative sign for cw turns.
© 2020-2021 Created by Tom Ruen