If p:a1.a2…am^n is a valid (closed) polytile, then p:a1.a2…am^nc is a degenerate c-cover of it, repeating the same vertices and edges c times. Multicovered polygons are degenerate and can’t be seen, but have a topological existence.
A c-cover polytile, p:a1.a2…am^nc, is written as a ''c''-compound '''c*p:a1.a2…am^n''', interpreted as ''c'' rotated copies of '''p:a1.a2…am^n'''. A c-compound m-adic nc-gram'' has mnc vertices.
Compounds like this were developed for regular star polygons, {p/q}. Like {6/2} has a direct interpretation as a double covered triangle, {3}, which is indivisible and degenerate. So {6/2} is reinterpreted as 2{3}, a compound of 2 triangles offset in orientation. So any reducible fraction {cp/cq} can become compound c{p/q}, and gcd(p,q)=1.
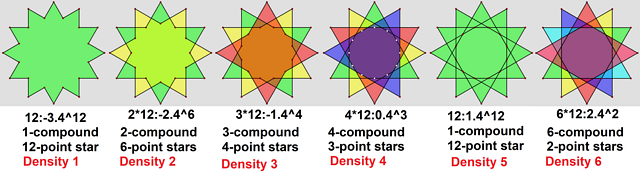 An example 12-pointed star, with density 1..6, 1 simple concave polygon, 4 compounds, and one star polygon. 12:-3.4^12, 2*12:-2.4^6, 3*12:-1.4^4, 4*12:0.4^3, 12:1.4^12, 6*12:2.4^2 |
© 2020-2021 Created by Tom Ruen