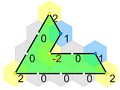
Regular (convex) Polytiles

An even sided regular polygon is 1^p, as a p-tile. An odd regular p-gon is 2^p, as a 2p-tile. Chains of odd-sided regular polygons could also be used to define p-tiles, but the possibilities are a subset of the even doubled 2p-tiles.

An even sided regular polygon is 1^p, as a p-tile. An odd regular p-gon is 2^p, as a 2p-tile. Chains of odd-sided regular polygons could also be used to define p-tiles, but the possibilities are a subset of the even doubled 2p-tiles.

In general a^b is a regular b-gon, as an ab-tile. A triangle can be a hexatile 2^3, octadecatile 3^3, or 6^3, dodecatile 4^3, etc. A square can be a tetratile 1^4, octatile 2^4, dodecatile 3^4, etc. A regular pentagon is 1^5 or 2^5. A hexagon can be hexatile 1^6, dodecatile 2^6, etc.

Set of regular polygons p=3-20

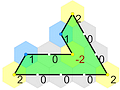
Regular (star and compound) Polytiles

A regular star polytile is of the form p:a^b, with ab/p turns, and c=gcd(a,p)=1.

If c>1, it can be remade into a c-compound as: c*p:a^(b/c). For example a pentagram, {5/2}, is 5:2^5, while a hexagram {6/2} is degenerate, but can be a 2-compound: 2{3} or 2*6:2^3.

Set of regular stars and compounds p=3-12

© 2020-2021 Created by Tom Ruen