Return to Home

Strictly Convex Polytiles

Enumeration

This table shows the enumeration of strictly-convex p-tiles, by sides with a brute-force search. Chiral pairs are counted as 1. Digon are excluded.

The highest-sided strictly convex p-tile is a regular p-gon. Identical polygons can repeat between p-tile families as multiplies. For instance, a square is the tetratile 1^4 and octatile 2^4, and dodecatile 3^4, etc.

You can see the counts generally increase exponentially, but not always consecutively. For instance there are more 24-tiles than 26-tiles, and more 30-tiles than 32 tiles.

Counts of convex p-tiles by sides
p	Total	Sides
p	Total	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40
4	1		1
6	3	1	1		1
8	4		2		1		1
10	7		2	1	2		1		1
12	16	1	3	1	4	1	3	1	1		1
14	17		3		4	1	4		3		1		1
16	28		4		5		8		5		4		1		1
18	70	1	4	1	9	4	12	6	12	4	9	1	4	1	1		1
20	85		5	1	8	1	16	2	17	2	16	1	8	1	5		1		1
22	125		5		10		20		26	1	26		20		10		5		1		1
24	392	1	6	2	15	8	33	20	50	27	66	27	50	20	33	8	15	2	6	1	1		1
26	379		6		14		35		57		76	1	76		57		35		14		6		1		1
28	704		7		16	1	47	1	79	3	126	4	134	4	126	3	79	1	47	1	16		7		1		1
30	3359	1	7	3	24	17	71	60	173	145	329	249	442	315	442	249	329	145	173	60	71	17	24	3	7	1	1		1
32	2248		8		21		72		147		280		375		440		375		280		147		72		21		8		1		1
34	4111		8		24		84		196		392		600		750	1	750		600		392		196		84		24		8		1		1
36	18510	1	9	3	32	21	116	90	322	260	775	599	1384	1073	2024	1392	2306	1392	2024	1073	1384	599	775	260	322	90	116	21	32	3	9	1	1		1
38	14309		9		9		30		120		324		756		1368		2052		2494	1	2494		2052		1368		756		324		120		30	0	9	0	1
40	30820	0	10	1	33	2	145	14	409	49	1036	147	2001	315	3300	521	4340	667	4838	667	4340	521	3300	315	2001	147	1036	49	409	14	145	2	33	1	10	0	1	0	1

Tetratiles, Hexatiles and Octatiles

There only one tetratile, a square, 1^4.
There are 3 hexatiles, a regular hexagon, 1^6, rhombus, 12^2, and an equilateral triangle, 2^3.
There are 4 octatiles: a regular octagon, 1^8, a flat hexagon 112^2, a square, 2^4, and a rhombus, 13^2.

Polytiles of the form a.b^2 are rhombi, alternating 2 angles.

Sets of convex tetratiles, hexatiles, and octatiles

Convex Tetratile
Sides	r8	Total
4	1	1
Total	1	1

Convex Hexatile
Sides	r12	r6	d4	Total
3		1		1
4			1	1
6	1			1
Total	1	1	1	3

Convex Octatile by sides and symmetry
Sides	r16	r8	i4	d4	Total
4		1		1	2
6			1		1
8	1				1
Total	1	1	1	1	4

Decatiles

There are 7 convex decatiles, grouped by sides:

[10] 1 regular decagon 1^10,
[5] 1 regular pentagon 2^5,
[8] 1 2111^2
[6] 2 221^2 and 311^2
[4] 2 rhombi: 32^2, and 41^2.

There is no special names for the irregular hexagons. The form a.(1^c)^2 , like 3.1.1^2 might be called a polygonal-lens, approximating 2 attached circular arcs.

Convex Decatiles by sides and symmetry
Sides	r20	r10	i4	d4	Total
4				2	2
5		1			1
6			2		2
8				1	1
10	1				1
Total	1	1	2	3	7

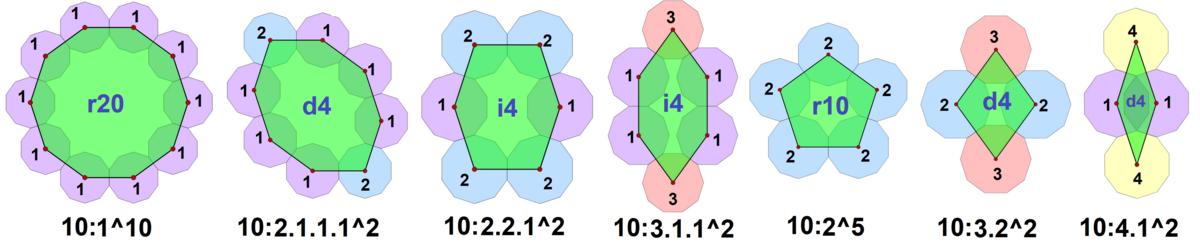
Set of convex decatiles

Dodecatiles

There are 16 convex dodecatiles, grouped by sides:

[12] 1 regular dodecagon, 1^12,
[10] 1 decagon 21111^2,
[9] 1 enneagon 211^3,
[8] 3 octagons 21^4, 2211^2, and 3111^2,
[7] 1 heptagon 1312131
[6] 3 hexagons: 2^6, 31^3, 411^2, (chiral pairs 123^2, 321^2)
[5] 1 pentagon: 41331
[4] 3 quadrilaterals: (square) 3^4, (and rhombi) 42^2, and 51^2,
[3] 1 equilateral triangle 4^3.

Polytiles of the form a.b^n are called isotoxal, having one edge type withing its symmetry, and 2 vertex types which alternate.

The decagon 21111^2 , octagon 3111^2, and hexagon 411^2 can be called polygonal-lens.

Convex Dodecatiles by sides and symmetry
Sides	r24	r12	r8	r6	p4	i6	i4	i2	d8	d6	d4	g2	Total
3				1									1
4			1								2		3
5								1					1
6		1					1			1		1	4
7								1					1
8					1				1		1		3
9						1							1
10							1						1
12	1												1
Total	1	1	1	1	1	1	2	2	1	1	3	1	16

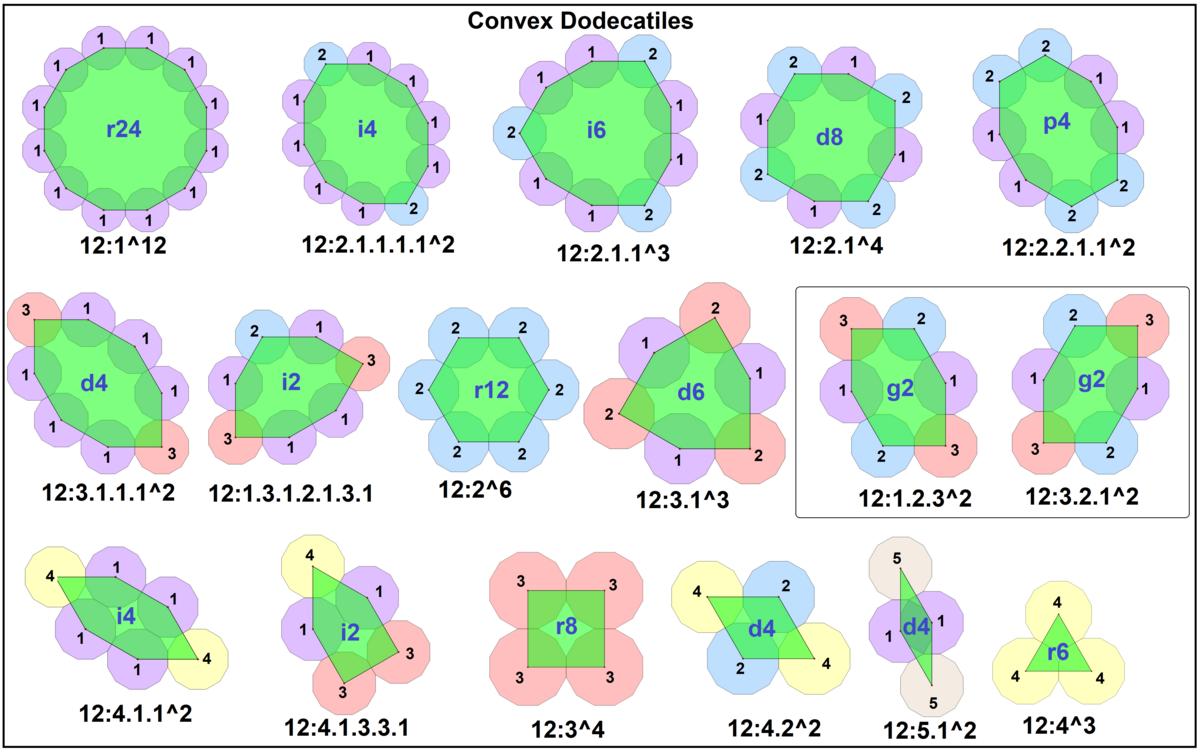
Set of convex dodecatiles

Tetradecatile

There are 17 tetradecatiles, grouped by sides:

[14] 14:1^14
[12] 14:111112^2
[10] 14:11113^2; 14:11122^2; 14:11212^2
[8] 14:1114^2; 14:1123^2; 14:1213^2; 14:1222^2
[7] 14:2^7
[6] 14:115^2; 14:124^2; 14:133^2; 14:223^2
[4] 14:16^2; 14:25^2; 14:34^2

Convex Tetradecatiles by sides and symmetry
Sides	r28	r14	i4	d4	g2	Total
4				3		3
6			3		1	4
7		1				1
8				3	1	4
10			3			3
12				1		1
14	1					1
Total	1	1	6	7	2	17

Hexadecatiles

There are 28 hexadecatiles, grouped by sides:

[16] 16:1^16
[14] 16:1111112^2
[12] 16:111113^2; 16:111122^2; 16:111212^2; 16:112112^2
[10] 16:11114^2; 16:11123^2; 16:11213^2; 16:11222^2; 16:12122^2
[8] 16:1115^2; 16:1124^2; 16:1133^2; 16:1214^2; 16:1223^2; 16:1232^2; 16:1313^2; 16:2^8
[6] 16:116^2; 16:125^2; 16:134^2; 16:224^2; 16:233^2
[4] 16:17^2; 16:26^2; 16:35^2; 16:4^4

Convex Hexadecatiles by sides and symmetry
Sides	r32	r16	r8	p4	i8	i4	d8	d4	g2	Total
4			1					3		4
6						3			2	5
8		1		1			1	3	2	8
10						3			2	5
12				1	1			2		4
14						1				1
16	1									1
Total	1	1	1	2	1	7	1	8	6	28

Octadecatiles

There are 70 octadecatiles, with 3,4,5,6,7,8,9,10,11,12,13,14,15,17,18 sides.

[18] 18:1^18
[16] 18:11111112^2
[15] 18:11112^3
[14] 18:1111113^2; 18:1111122^2; 18:1111212^2; 18:1112112^2
[13] 18:1111221121113
[12] 18:111114^2; 18:111123^2; 18:111213^2; 18:111222^2; 18:1113^3; 18:112113^2; 18:112122^2; 18:1122^3; 18:121212^2
[11] 18:11114112114; 18:11122221114; 18:11131221123; 18:11222113113
[10] 18:11115^2; 18:11124^2; 18:11133^2; 18:1114113114; 18:11214^2; 18:1122222114; 18:11223^2; 18:11232^2; 18:11313^2; 18:12123^2; 18:12213^2; 18:12222^2
[9] 18:111422115; 18:112411314; 18:113222214; 18:114^3; 18:123^3; 18:2^9
[8] 18:1116^2; 18:1125^2; 18:1134^2; 18:11414115; 18:11422224; 18:1215^2; 18:1224^2; 18:1233^2; 18:1242^2; 18:1314^2; 18:1323^2; 18:2223^2
[7] 18:1144116; 18:1152225; 18:1242315; 18:1414224
[6] 18:117^2; 18:126^2; 18:135^2; 18:144^2; 18:15^3; 18:225^2; 18:234^2; 18:24^3; 18:3^6
[5] 18:15426
[4] 18:18^2; 18:27^2; 18:36^2; 18:45^2
[3] 18:6^3

Convex Octadecatiles by sides and symmetry
Sides	r36	r18	r12	r6	p6	p2	i6	i4	i2	d12	d6	d4	d2	g3	g2	a1	Total
3				1													1
4												4					4
5																1	1
6			1					3			2				3		9
7									3							1	4
8						1						6	1		4		12
9		1					1							1		3	6
10								6					2		4		12
11									3							1	4
12					1					1	1	3			3		9
13																1	1
14								4									4
15							1										1
16												1					1
18	1																1
Total	1	1	1	1	1	1	2	13	6	1	3	14	3	1	14	7	70

Icosatiles

There are 85 icosatiles, grouped by sides:

[20] 20:1^20
[18] 20:111111112^2
[16] 20:11111113^2; 20:11111122^2; 20:11111212^2; 20:11112112^2; 20:11121112^2
[15] 20:112^5
[14] 20:1111114^2; 20:1111123^2; 20:1111213^2; 20:1111222^2; 20:1112113^2; 20:1112122^2; 20:1121122^2; 20:1121212^2
[13] 20:1121131211213
[12] 20:111115^2; 20:111124^2; 20:111133^2; 20:111214^2; 20:111223^2; 20:111232^2; 20:111313^2; 20:112114^2; 20:112123^2; 20:112132^2; 20:112213^2; 20:112222^2; 20:113113^2; 20:121213^2; 20:121222^2; 20:122122^2
[11] 20:11214121133; 20:11313121313
[10] 20:11116^2; 20:11125^2; 20:11134^2; 20:11215^2; 20:11224^2; 20:11233^2; 20:11242^2; 20:11314^2; 20:11323^2; 20:12124^2; 20:12133^2; 20:12214^2; 20:12223^2; 20:12232^2; 20:12313^2; 20:13^5; 20:2^10
[9] 20:113412143; 20:131331314
[8] 20:1117^2; 20:1126^2; 20:1135^2; 20:1144^2; 20:1216^2; 20:1225^2; 20:1234^2; 20:1243^2; 20:1252^2; 20:1315^2; 20:1324^2; 20:1333^2; 20:1414^2; 20:2224^2; 20:2233^2; 20:2323^2
[7] 20:1343144
[6] 20:118^2; 20:127^2; 20:136^2; 20:145^2; 20:226^2; 20:235^2; 20:244^2; 20:334^2
[5] 20:4^5
[4] 20:19^2; 20:28^2; 20:37^2; 20:46^2; 20:5^4

Convex Icosatiles by sides and symmetry
Sides	r40	r20	r10	r8	p4	i10	i8	i4	i2	d10	d8	d4	g2	Total
4				1								4		5
5			1											1
6								4					4	8
7									1					1
8					2						2	6	6	16
9									2					2
10		1						5		1			10	17
11									2					2
12					2		2					6	6	16
13									1					1
14								4					4	8
15						1								1
16					2						1	2		5
18								1						1
20	1													1
Total	1	1	1	1	6	1	2	14	6	1	3	18	30	85

22-tiles

There are 125 22-tiles.

Convex 22-tiles by sides and symmetry
Sides	r44	r22	i4	d4	g2	Total
4				5		5
6			5		5	10
8				10	10	20
10			10		16	26
11		1				1
12				10	16	26
14			10		10	20
16				5	5	10
18			5			5
20				1		1
22	1					1
Total	1	1	30	31	62	125

24-tiles

There are 392 24-tiles.

Convex 24-tiles by sides and symmetry
Sides	r48	r24	r16	r12	r8	p8	p6	p4	p2	i12	i8	i6	i4	i2	d16	d12	d8	d6	d4	d2	g4	g3	g2	a1	Total
4					1														5						6
5														1										1	2
6				1									4					3					7		15
7														4										4	8
8			1					2	1								2		10	1			14	2	33
9												3		3								2		12	20
10									1				10							8			28	3	50
11														8										19	27
12		1					1	4	1		1					1		3	13	1	1	2	29	8	66
13														8										19	27
14									2				10							7			28	3	50
15												3		3								2		12	20
16						1		4	1						1		1		8	1			14	2	33
17														4										4	8
18							1			1			4					2					7		15
19														1										1	2
20								2			1								3						6
21												1													1
22													1												1
24	1																								1
Total	1	1	1	1	1	1	2	12	6	1	2	7	29	32	1	1	3	8	39	18	1	6	127	90	391

26-tiles

There are 379 26-tiles.

Convex 26-tiles by sides and symmetry
Sides	r52	r26	i4	d4	g2	Total
4				6		6
6			6		8	14
8				15	20	35
10			15		42	57
12				20	56	76
13		1				1
14			20		56	76
16				15	42	57
18			15		20	35
20				6	8	14
22			6			6
24				1		1
26	1					1
Total	1	1	62	63	252	379

28-tiles

There are 704 28-tiles.

**Convex 28-tiles** by sides and symmetry
Sides	r56	r28	r14	r8	p4	i14	i8	i4	i2	d14	d8	d4	g4	g2	a1	Total
4				1								6				7
6								6						10		16
7			1													1
8					3						3	15		26		47
9									1							1
10								15						64		79
11									3							3
12					6		3					26	1	90		126
13									3						1	4
14		1						19		1				113		134
15									3						1	4
16					10						3	22	1	90		126
17									3							3
18								15						64		79
19									1							1
20					6		3					12		26		47
21						1										1
22								6						10		16
24					3						1	3				7
26								1								1
28	1															1
Total	1	1	1	1	28	1	6	62	14	1	7	84	2	493	2	704

30-tiles

There are 3359 30-tiles.

Convex 30-tiles by sides and symmetry
Sides	r60	r30	r20	r12	r10	r6	p10	p6	p2	i12	i10	i6	i4	i2	d20	d12	d10	d6	d4	d2	g5	g3	g2	a1	Total
3						1																			1
4																			7						7
5					1																			2	3
6				1									6					4		1			12		24
7														8										9	17
8									3										21	4			35	8	71
9												4		6								4		46	60
10			1						2				20				2			20			90	38	173
11														23										122	145
12								2	11							2		6	33	13		6	150	106	329
13														25										224	249
14									8				35							36			197	166	442
15		1									1	5		30							1	10		267	315
16									20										35	24			197	166	442
17														25										224	249
18								2	6	2			33					6		18		6	150	106	329
19														23										122	145
20							1		12						1		1		20	10			90	38	173
21												4		6								4		46	60
22									2				21							5			35	8	71
23														8										9	17
24								2	1							1		2	6				12		24
25											1													2	3
26													7												7
27												1													1
28																			1						1
30	1																								1
Total	1	1	1	1	1	1	1	6	65	2	2	14	122	154	1	3	3	18	123	131	1	30	968	1709	3359

32-tiles

There are 2248 32-tiles:

Convex 32-tiles by sides and symmetry
Sides	r64	r32	r16	r8	p8	p4	i16	i8	i4	d16	d8	d4	g4	g2	Total
4				1								7			8
6									7					14	21
8			1			3					3	21		44	72
10									21					126	147
12						9		3				44	2	222	280
14									35					340	375
16		1			1	16				1	3	48	2	368	440
18									35					340	375
20						16		3				37	2	222	280
22									21					126	147
24					1	9	1				2	15		44	72
26									7					14	21
28						3		1				4			8
30									1						1
32	1														1
Total	1	1	1	1	2	56	1	7	127	1	8	176	6	1860	2248

34-tiles

There are 4111 34-tiles:

36-tiles

There are 18510 36-tiles

38-tiles

There are 14309 38-tiles

40-tiles

There are 30820 40-tiles

Equilateral triangles

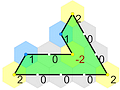
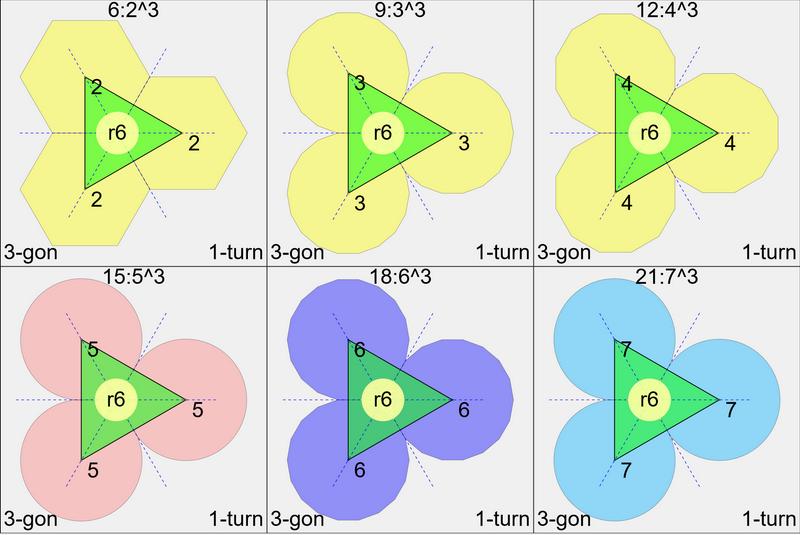
The only equilateral triangle is regular. It can be constructed as 3k-tiles: k^3, shown for 6,9,12,15,18,21.

Squares and rhombi

For a given p-tiles, there are int(p/2) rhombi, p:a.b^2, where p=2(a+b). If p/2 is even, one of them is a square. A rhombus has d4 symmetry.

Sets of rhombi, p=4..12

Pentagons

There are a relatively few number of strictly-convex equilateral pentagons. All of them besides a regular pentagon can be dissected into an equilateral triangle of a rhombus, so only occur for p-tiles with p as a multiple of 3. The only equilateral pentagon with bilateral symmetry, i2, is 12:4.1.3.3.1, as a triangle and square. The remainder have no symmetry, a1.

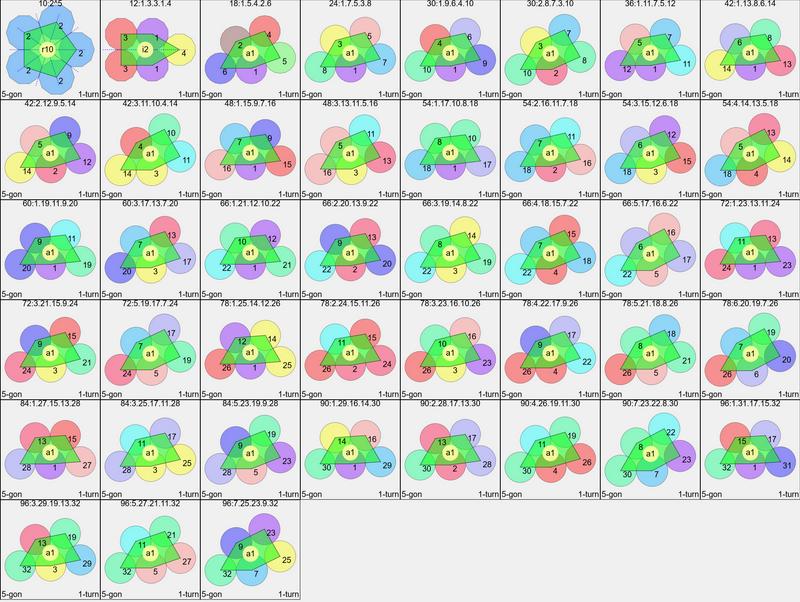
Set of convex equilateral pentagons, p=4...100

Near-misses

There are a few near-misses, given a more generous tolerance for closing.

These can be considered partial polytiles, with one edge length non-unit length, and two angles not quite whole divisors of a full circle

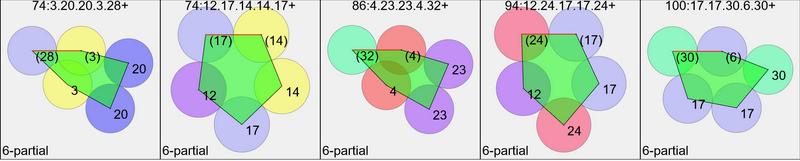
Near-miss pentagonal polytiles

Hexagons

Heptagons

Lenses

Here, a convex lens polytile can be seen in the form p:a.(1^b)^2, with p=2(a+b). Lenses can only have an even number of sides, specifically a 2(1+b)-gon. If b=1, a lens is a rhombus. When a=1, it becomes regular. The largest nonregular lenses, a=2, are (p-2)-gons. A lens will have either d4 or i4 symmetry, depending on the number of sides.

A lens can be constructed as an extended digon: 2k:k^2!(1^b), where b=1...k.

Set of lenses, a=2, p=4..16

Trilenses

A convex trilens polytile can be seen of the form p:a.(1^b)^3, with p=3(a+b). Trilenses have sides as a multiple of 3, specifically 3(1+b)-gon. If b=0, it is a triangle. If b=1, it is an isotoxal hexagon. If a=1, it becomes regular. The largest nonregular trilenses, a=2, are (p-3)-gons. A trilens will have either d6 or i6 symmetry, depending on the number of sides.

A trilens can be construcated as an extended triangle: 3k:k^3!(1^b), where b=1..k.

This can generalize into a k-lens of the form p:a.(1^b)^k, where p=k(a+b).

Set of trilenses

Orthogons

Here a convex orthogon is defined as a convex polygon with two orthogonal lines of reflection. There are int(p/4) strictly-convex orthogons among the strictly convex p-tiles. They can have symmetry p4,i4,d4. A p-tile orthogon is a (p-4)-gon.

Set of orthogons