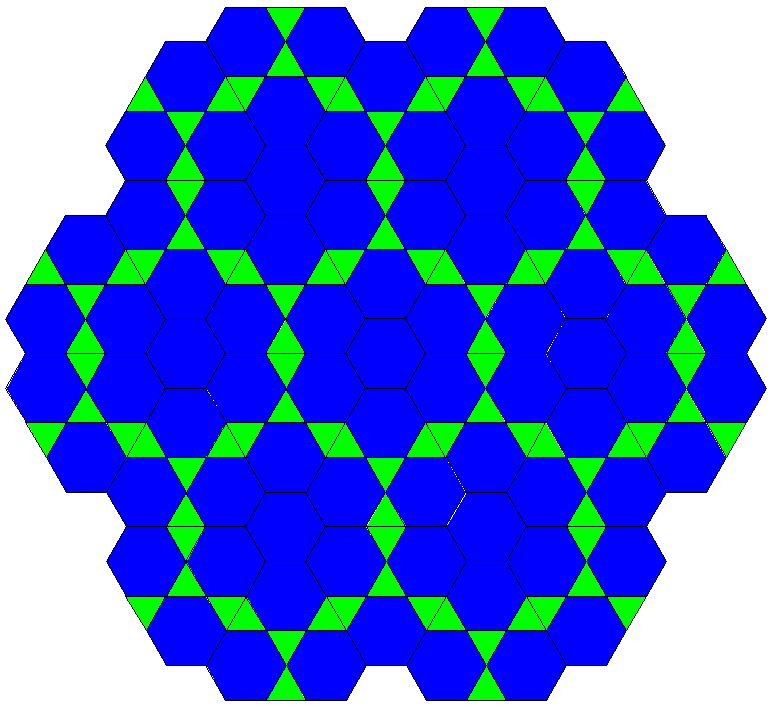
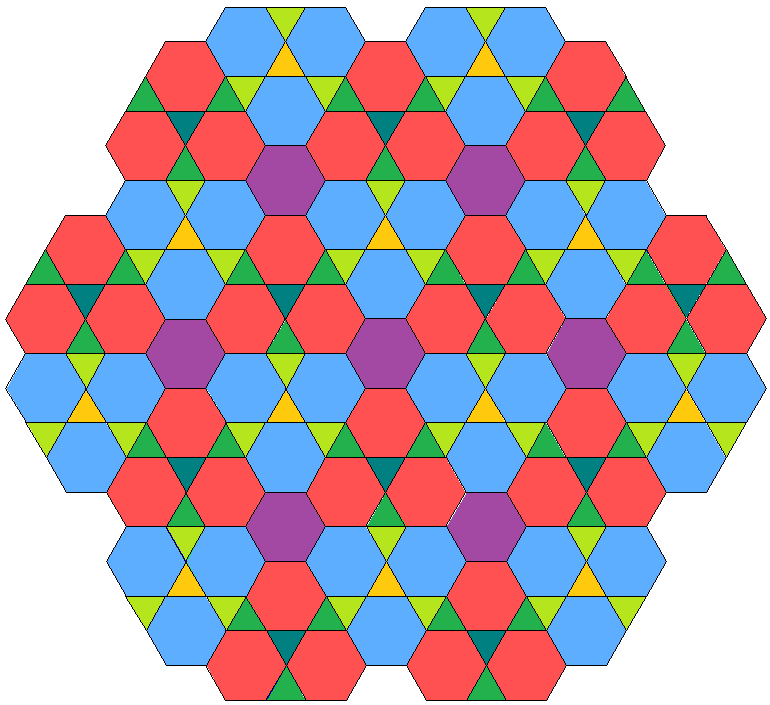
- uniform relative:
- trat that hexat
- related CRF tilings:
- ((uBxx3xoAo3xooA3*a))&#zx
- related rhomb tiling:
- rhombic ((uBxx3uxBx3xooA3*a))&#zx
| Acronym | ... |
| Name | partially contracted hexagonal tiling |


| |
| Vertex figure | [63], [32,62], [(3,6)2] |
| Confer |
|
Trat could be considered as a vertex overlay of hexat plus 3 shifted copies of trats with edge size 3 (see there). This decomposition allows for a 3-step transformation running then through ((uBxx3xoAo3xooA3*a))&#zx and this tiling towards a pure hexat (A = 3x, B = 4x). – So this transformation sequence is not a true partial Stott expansion one because pairs of triangles become transformed into single hexagons. But this could be recovered by combining these pairs into rhombs. The corresponding sequence member here then would be rhombic ((uBxx3uxBx3xooA3*a))&#zx.
Incidence matrix according to Dynkin symbol
((uBxx3uxBx3xooA3*a))&#zx (N → ∞, A = 3x, B = 4x) o...3o...3o...3*a | 6N * * * | 1 1 1 1 0 0 0 0 | 1 1 1 1 0 0 0 [32,62] .o..3.o..3.o..3*a | * 3N * * | 0 2 0 0 2 0 0 0 | 1 0 2 0 1 0 0 [(3,6)2] ..o.3..o.3..o.3*a | * * 3N * | 0 0 2 0 0 2 0 0 | 0 1 0 2 0 1 0 [(3,6)2] ...o3...o3...o3*a | * * * 6N | 0 0 0 1 0 0 1 1 | 0 0 1 1 0 0 1 [63] ----------------------+-------------+-------------------------+------------------ .... .... x... | 2 0 0 0 | 3N * * * * * * * | 1 1 0 0 0 0 0 oo..3oo..3oo..3*a | 1 1 0 0 | * 6N * * * * * * | 1 0 1 0 0 0 0 o.o.3o.o.3o.o.3*a | 1 0 1 0 | * * 6N * * * * * | 0 1 0 1 0 0 0 o..o3o..o3o..o3*a | 1 0 0 1 | * * * 6N * * * * | 0 0 1 1 0 0 0 .... .x.. .... | 0 2 0 0 | * * * * 3N * * * | 0 0 1 0 1 0 0 ..x. .... .... | 0 0 2 0 | * * * * * 3N * * | 0 0 0 1 0 1 0 ...x .... .... | 0 0 0 2 | * * * * * * 3N * | 0 0 0 1 0 0 1 .... ...x .... | 0 0 0 2 | * * * * * * * 3N | 0 0 1 0 0 0 1 ----------------------+-------------+-------------------------+------------------ .... .... xo.. &#x | 2 1 0 0 | 1 2 0 0 0 0 0 0 | 3N * * * * * * .... .... x.o. &#x | 2 0 1 0 | 1 0 2 0 0 0 0 0 | * 3N * * * * * .... ux.x .... &#xt | 2 2 0 2 | 0 2 0 2 1 0 0 1 | * * 3N * * * * u.xx .... .... &#xt | 2 0 2 2 | 0 0 2 2 0 1 1 0 | * * * 3N * * * .... .x..3.o.. | 0 3 0 0 | 0 0 0 0 3 0 0 0 | * * * * N * * ..x. .... ..o.3*a | 0 0 3 0 | 0 0 0 0 0 3 0 0 | * * * * * N * ...x3...x .... | 0 0 0 6 | 0 0 0 0 0 0 3 3 | * * * * * * N
or o...3o...3o...3*a | 6N * * | 1 2 1 0 0 | 2 2 0 0 [32,62] .o..3.o..3.o..3*a & | * 6N * | 0 2 0 2 0 | 1 2 1 0 [(3,6)2] ...o3...o3...o3*a | * * 6N | 0 0 1 0 2 | 0 2 0 1 [63] ------------------------+----------+-----------------+----------- .... .... x... | 2 0 0 | 3N * * * * | 2 0 0 0 oo..3oo..3oo..3*a & | 1 1 0 | * 12N * * * | 1 1 0 0 o..o3o..o3o..o3*a | 1 0 1 | * * 6N * * | 0 2 0 0 .... .x.. .... & | 0 2 0 | * * * 6N * | 0 1 1 0 ...x .... .... & | 0 0 2 | * * * * 6N | 0 1 0 1 ------------------------+----------+-----------------+----------- .... .... xo.. &#x & | 2 1 0 | 1 2 0 0 0 | 6N * * * .... ux.x .... &#xt & | 2 2 2 | 0 2 2 1 1 | * 6N * * .... .x..3.o.. & | 0 3 0 | 0 0 0 3 0 | * * 2N * ...x3...x .... | 0 0 6 | 0 0 0 0 6 | * * * N
© 2004-2026 | top of page |