rhombic ((uBxx3uxBx3xooA3*a))&#zx
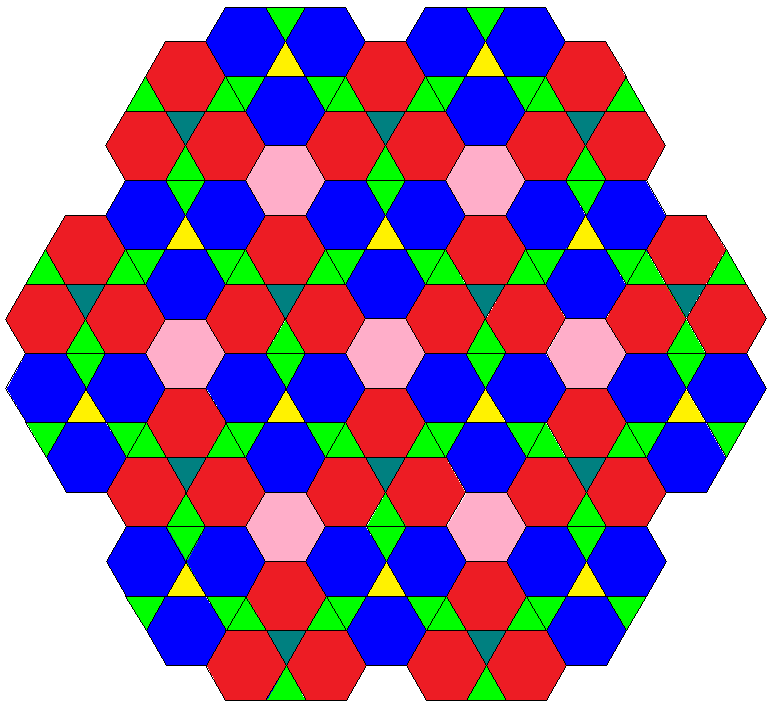
- uniform relative:
- trat that hexat
- related CRF tilings:
- ((uBxx3uxBx3xooA3*a))&#zx
- related rhomb tiling:
- rhombic ((uBxx3xoAo3xooA3*a))&#zx
- general polytopal classes:
- partial Stott expansions
| Acronym | ... |
| Name |
partially contracted hexagonal tiling, rhombic ((uBxx3uxBx3xooA3*a))&#zx |

| |
| Vertex figure | [63], [62,R], [3,6,r,6] |
| Confer |
|
Both, trat and the tri-hexagonal rhombic tiling (derived from the former by combining 2 triangles each) could be considered as a vertex overlay of hexat plus 3 shifted copies of trats with edge size 3 (see there). This decomposition allows for a 3-step partial Stott expansion of the latter running then through rhombic ((uBxx3xoAo3xooA3*a))&#zx and this tiling towards a pure hexat (A = 3x, B = 4x).
Incidence matrix according to Dynkin symbol
(rhombic) ((uBxx3uxBx3xooA3*a))&#zx (N → ∞, A = 3x, B = 4x) o...3o...3o...3*a | 6N * * * | 1 1 1 0 0 0 0 | 1 1 1 0 0 0 [62,R] .o..3.o..3.o..3*a | * 3N * * | 2 0 0 2 0 0 0 | 1 2 0 1 0 0 [3,6,r,6] ..o.3..o.3..o.3*a | * * 3N * | 0 2 0 0 2 0 0 | 1 0 2 0 1 0 [3,6,r,6] ...o3...o3...o3*a | * * * 6N | 0 0 1 0 0 1 1 | 0 1 1 0 0 1 [63] ----------------------+-------------+----------------------+--------------- oo..3oo..3oo..3*a | 1 1 0 0 | 6N * * * * * * | 1 1 0 0 0 0 o.o.3o.o.3o.o.3*a | 1 0 1 0 | * 6N * * * * * | 1 0 1 0 0 0 o..o3o..o3o..o3*a | 1 0 0 1 | * * 6N * * * * | 0 1 1 0 0 0 .... .x.. .... | 0 2 0 0 | * * * 3N * * * | 0 1 0 1 0 0 ..x. .... .... | 0 0 2 0 | * * * * 3N * * | 0 0 1 0 1 0 ...x .... .... | 0 0 0 2 | * * * * * 3N * | 0 0 1 0 0 1 .... ...x .... | 0 0 0 2 | * * * * * * 3N | 0 1 0 0 0 1 ----------------------+-------------+----------------------+--------------- .... .... xoo. &#xt | 2 1 1 0 | 2 2 0 0 0 0 0 | 3N * * * * * .... ux.x .... &#xt | 2 2 0 2 | 2 0 2 1 0 0 1 | * 3N * * * * u.xx .... .... &#xt | 2 0 2 2 | 0 2 2 0 1 1 0 | * * 3N * * * .... .x..3.o.. | 0 3 0 0 | 0 0 0 3 0 0 0 | * * * N * * ..x. .... ..o.3*a | 0 0 3 0 | 0 0 0 0 3 0 0 | * * * * N * ...x3...x .... | 0 0 0 6 | 0 0 0 0 0 3 3 | * * * * * N
or o...3o...3o...3*a | 6N * * | 2 1 0 0 | 1 2 0 0 [62,R] .o..3.o..3.o..3*a & | * 6N * | 2 0 2 0 | 1 2 1 0 [3,6,r,6] ...o3...o3...o3*a | * * 6N | 0 1 0 2 | 0 2 0 1 [63] ------------------------+----------+--------------+----------- oo..3oo..3oo..3*a & | 1 1 0 | 12N * * * | 1 1 0 0 o..o3o..o3o..o3*a | 1 0 1 | * 6N * * | 0 2 0 0 .... .x.. .... & | 0 2 0 | * * 6N * | 0 1 1 0 ...x .... .... & | 0 0 2 | * * * 6N | 0 1 0 1 ------------------------+----------+--------------+----------- .... .... xoo. &#xt | 2 2 0 | 4 0 0 0 | 3N * * * u.xx .... .... &#xt | 2 2 2 | 2 2 1 1 | * 6N * * .... .x..3.o.. & | 0 3 0 | 0 0 3 0 | * * 2N * ...x3...x .... | 0 0 6 | 0 0 0 6 | * * * N
© 2004-2026 | top of page |