 ©
©| Acronym | ... |
| Name |
octagonal Leonardo style "polyhedron of renaissance", vertex figure of lamina-trunc(o8o4xb3x) |
| Circumradius | sqrt[2+sqrt(2)] = 1.847759 |
| Face vector | 26, 56, 32 |
using edge sizes x = 1 and q = sqrt(2) = 1.414214
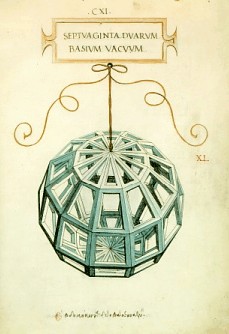
Leonardo da Vinci himself drew a dodecagonal variant thereof, cf. at right. In fact, in both cases the equatorial polygon is chosen identical to the meridian ones, providing vertices at the equator as well as at the poles, and possibly further ones along some circles of latitude. Thus the n-gonality here requires n=4m. His one then is the case m=3, the one provided here is m=2, and the case m=1 would be oct.
This case of m=2 is special (beyond the trivial case of m=1) in providing only chords of regular polygons for edges. Thus it can be used as vertex figure for this uniform hyperbolic laminate honeycomb lamina-trunc(o8o4xb3x).
Incidence matrix according to Dynkin symbol
oxqxo8ooooo&#qt → inner heights = sqrt(1+1/sqrt(2)) = 1.306563
outer heights = sqrt(4-2 sqrt(2)) = 1.082392
o....8o.... | 1 * * * * | 8 0 0 0 0 0 0 | 8 0 0 0
.o...8.o... | * 8 * * * | 1 2 1 0 0 0 0 | 2 2 0 0
..o..8..o.. | * * 8 * * | 0 0 1 2 1 0 0 | 0 2 2 0
...o.8...o. | * * * 8 * | 0 0 0 0 1 2 1 | 0 0 2 2
....o8....o | * * * * 1 | 0 0 0 0 0 0 8 | 0 0 0 8
---------------+-----------+---------------+--------
oo...8oo...&#q | 1 1 0 0 0 | 8 * * * * * * | 2 0 0 0
.x... ..... | 0 2 0 0 0 | * 8 * * * * * | 1 1 0 0 x
.oo..8.oo..&#q | 0 1 1 0 0 | * * 8 * * * * | 0 2 0 0
..q.. ..... | 0 0 2 0 0 | * * * 8 * * * | 0 1 1 0
..oo.8..oo.&#q | 0 0 1 1 0 | * * * * 8 * * | 0 0 2 0
...x. ..... | 0 0 0 2 0 | * * * * * 8 * | 0 0 1 1 x
...oo8...oo&#q | 0 0 0 1 1 | * * * * * * 8 | 0 0 0 2
---------------+-----------+---------------+--------
ox... .....&#q | 1 2 0 0 0 | 2 1 0 0 0 0 0 | 8 * * *
.xq.. .....&#q | 0 2 2 0 0 | 0 1 2 1 0 0 0 | * 8 * *
..qx. .....&#q | 0 0 2 2 0 | 0 0 0 1 2 1 0 | * * 8 *
...xo .....&#q | 0 0 0 2 1 | 0 0 0 0 0 1 2 | * * * 8
((abo oxq8ooo))&#zq → heights = 0
a = 2 sqrt(2+sqrt(2)) = 3.695518
b = a/q = sqrt(4+2 sqrt(2)) = 2.613126
(tegum sum of a-line, (x,b)-op, and q-{8})
o.. o..8o.. | 2 * * | 8 0 0 0 | 8 0
.o. .o.8.o. | * 16 * | 1 2 1 0 | 2 2
..o ..o8..o | * * 8 | 0 0 2 2 | 0 4
---------------+--------+------------+------
oo. oo.8oo.&#q | 1 1 0 | 16 * * * | 2 0
... .x. ... | 0 2 0 | * 16 * * | 1 1 x
.oo .oo8.oo&#q | 0 1 1 | * * 16 * | 0 2
... ..q ... | 0 0 2 | * * * 8 | 0 2
---------------+--------+------------+------
... ox. ...&#q | 1 2 0 | 2 1 0 0 | 16 *
... .xq ...&#q | 0 2 2 | 0 1 2 1 | * 16
© 2004-2026 | top of page |