| Site Map | Polytopes | Dynkin Diagrams | Vertex Figures, etc. | Incidence Matrices | Index |
One might ask, whether it is possible to provide a regular polygon as a continuous curve, possibly given in polar coordinates?
Indeed, this is an easy exercise. We just need some values from the page on the general regular polygon:
| Dynkin diagram | x-n/d-o |
| Schläfli symbol | {n/d} |
| Circumradius | 1/(2 sin(π d/n)) |
| Inradius | 1/(2 tan(π d/n)) |

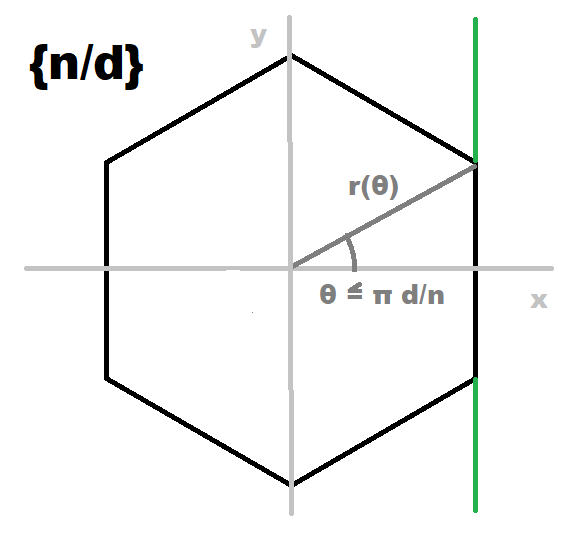
First consider a vertical side for some positive x.
From x = r cos(θ) we obviously get r(θ) = x / cos(θ).
As that side will be centered at its midpoint at the distance of the inradius, one further has x = 1/(2 tan(π d/n)).
Thus this correctly displaced vertical line would be given within polar coordinates as
r(θ) = 1/[2 tan(π d/n) cos(θ)]
Next one has to determine the 2 vertices of this side.
These will be given at θ = ±π d/n, up and down from the x-axis.
The remainder then just is to apply that very angular region over and over again periodically.
r(θ) = 1/[2 tan(π d/n) cos(θ - 2π d/n floor[(θ n + π d)/(2π d)])]
(where floor(x) = x - (x mod 1), for sure).
© 2004-2025 | top of page |