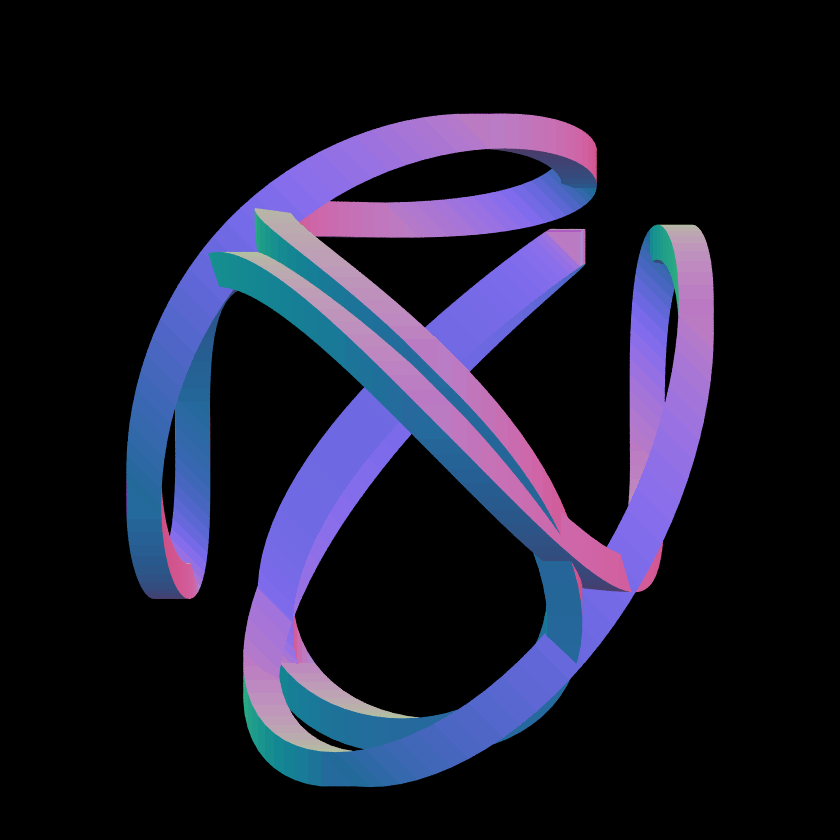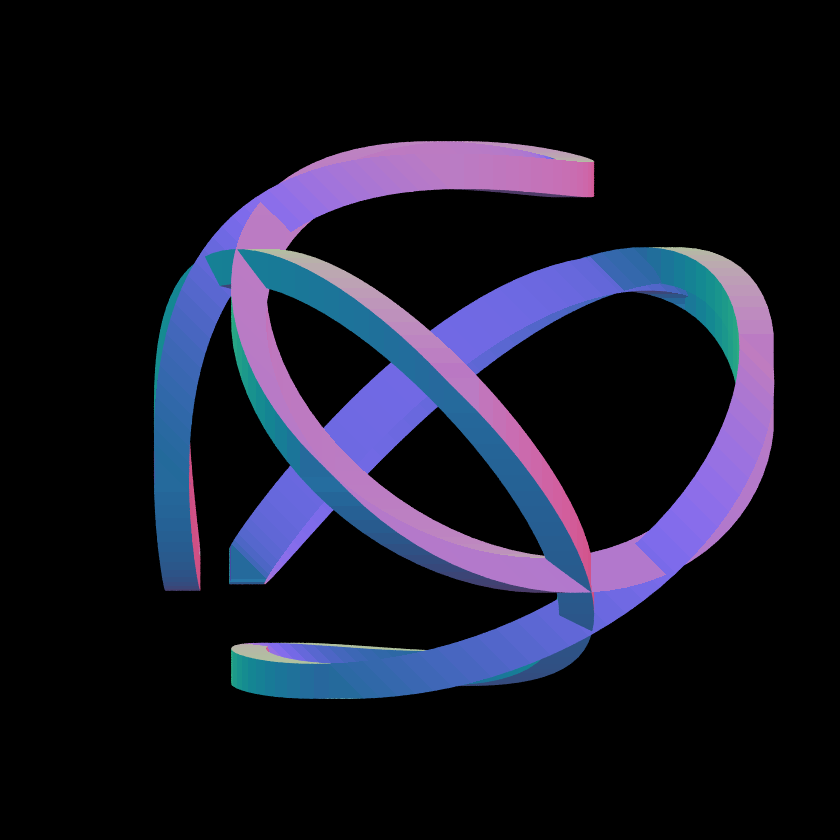How many Euler circuits are there in the complete directed graph on N vertices?
More interesting to me, how many equivalence classes under reversal and relabeling?
| N | circuits | classes |
| 3 | 3 | 1 |
| 4 | 256 | 6 |
| 5 | 972000 | 4089 |
| 6 | 247669456896 | … |
As I write this I am waiting for my program to finish counting the classes for N=6, and I see how I could make it speedier (not that I’ll ever want to run it again when it’s done). After all sequences beginning 010 have been generated, it ought to skip any further subsequences that contain u-turns, like 01202 (on which it wasted hours), because these are equivalent to some 010 sequence.
I made models of the six N=4 cases (and tried to put them on Thingiverse and Thangs, but no images show up). The vertices are those of a tetrahedron, of course. I knew from the start that the corners of the path ought to be smoothed, to make it easier to follow; my favorite design so far is a Fourier series (six components) that matches the derivative at the midpoint of each edge. They look like martian game-pieces. I was surprised to find that all of them have u-turns.
Loosening the rules, to allow the path to include an edge twice in the same direction, gives 15 more classes (of which three have no u-turns). I may have those printed later in a contrasting color.