Ridge-facetings of the icosidodecahedron ship

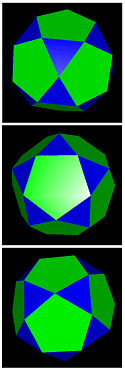
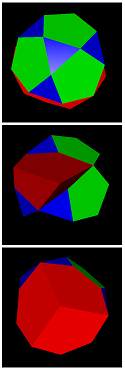
Possible facets here are the 20 triangles and 12 pentagons of the comodore itself together with the 6 internal decagons. The general naming code here is accordingly id-#{3}-#{5}-#{10}. This gives rise for exactly 7 edge-facetings with n-gonal axial rotation symmetries, provided n > 2. In fact, 3 have full icosahedral symmetry, 2 have 5-fold pyramidal symmetry, and 2 have 3-fold pyramidal symmetry.

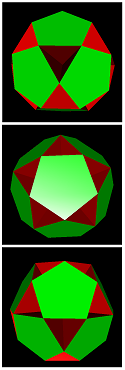
id-20-12-0 = id	id-20-0-6 = seihid	id-0-12-6 = sidhid	id-10-6-1 = pero	id-10-6-5 = pegger	id-10-6-3-a = idtef	id-10-6-3-b = idger
icosahedral			5-fold pyramidal		3-fold pyramidal

Ridge-facetings of the great icosidodecahedron ship

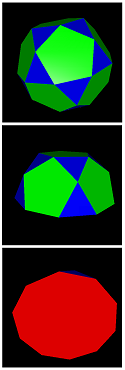
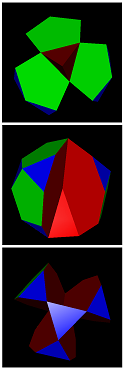
Possible facets here are the 12 pentagrams and 20 triangles of the comodore itself together with the 6 internal decagrams. The general naming code here is accordingly gid-#{5/2}-#{3}-#{10/3}. This gives rise for exactly 7 edge-facetings with n-gonal axial rotation symmetries, provided n > 2. In fact, 3 have full icosahedral symmetry, 2 have 5-fold pyramidal symmetry, and 2 have 3-fold pyramidal symmetry.

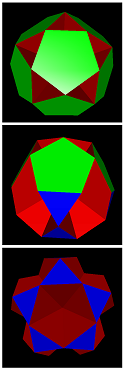
gid-12-20-0 = gid	gid-12-0-6 = gidhid	gid-0-20-6 = geihid	gid-6-10-1 = sisro	gid-6-10-5 = stagger	gid-6-10-3-a = gidtef	gid-6-10-3-b = gidger
icosahedral			5-fold pyramidal		3-fold pyramidal