Ridge-facetings of the great dodekicosidodecahedron ship

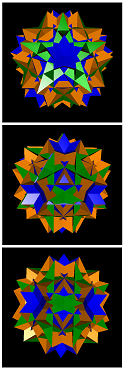
Possible facets here are the 12 pentagrams, 20 triangles, and 12 decagrams of the comodore itself together with the 30 internal squares. The general naming code here is accordingly gaddid-#{5/2}-#{3}-#{10/3}-#{4}. This gives rise for exactly 30 edge-facetings with n-gonal axial rotation symmetries, provided n > 2. In fact, 3 have full icosahedral symmetry, 10 have 5-fold pyramidal symmetry, 3 have 5-fold antiprismatic symmetry, 11 have 3-fold pyramidal symmetry, and 3 have 3-fold antiprismatic symmetry.

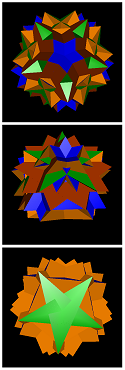
gaddid-12-20-12-0 = gaddid	gaddid-12-20-0-30 = qrid	gaddid-0-0-12-30 = gird	gaddid-1-5-1-5 = rastacu	gaddid-1-5-11-25	gaddid-5-5-5-15	gaddid-5-5-7-15	gaddid-6-10-6-10-a
icosahedral			5-fold pyramidal ...
gaddid-6-10-6-10-b	gaddid-6-10-6-20	gaddid-7-15-5-15	gaddid-11-15-1-25	gaddid-11-15-11-5	gaddid-2-10-10-20	gaddid-10-10-2-20	gaddid-10-10-10-10
... 5-fold pyramidal					5-fold antiprismatic
gaddid-3-7-3-9	gaddid-3-7-9-21	gaddid-3-15-9-15	gaddid-6-10-6-12-a	gaddid-6-10-6-12-b	gaddid-6-10-6-18-a	gaddid-6-10-6-18-b	gaddid-9-5-3-15
3-fold pyramidal ...
gaddid-9-5-9-15	gaddid-9-13-3-21	gaddid-9-13-9-9	gaddid-6-6-6-12	gaddid-6-6-6-18	gaddid-6-14-6-12
... 3-fold pyramidal			3-fold antiprismatic