|
Acronym
|
toe (alt.: gratet)
|
|
TOCID symbol
|
tO, tTT
|
|
Name
|
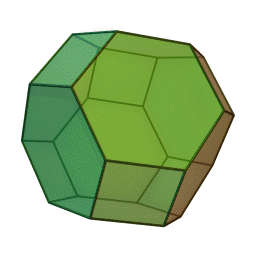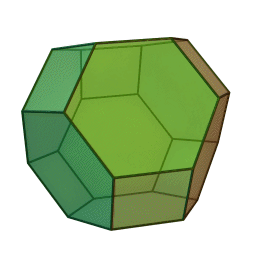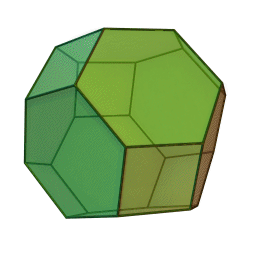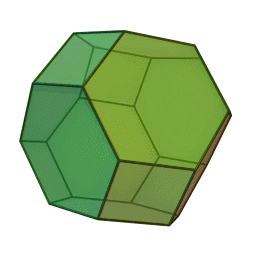
truncated octahedron,
omnitruncated tetrahedron,
great rhombitetratetrahedron,
Voronoi cell of body-centered cubic (bcc) lattice,
Kelvin's tetrakaidecahedron,
Waterman polyhedron number 10 wrt. face-centered cubic lattice A3 centered at a lattice point,
permutohedron of 4 elements
|
|
|
 © © © ©  © ©
|
|
Circumradius
|
sqrt(5/2) = 1.581139
|
Inradius
wrt. {4}
|
sqrt(2) = 1.414214
|
Inradius
wrt. {6}
|
sqrt(3/2) = 1.224745
|
|
Vertex figure
|
[4,62] = qo&#h
|
|
Snub derivation
|
|
|
Vertex layers
|
| x3x4o | x3x .
{6} first | x . o
edge first | . x4o
{4} first |
| u3x . | u . q | . u4o |
| x3u . | w . o | . x4q |
| x . Q |
x3x .
opposite {6} | w . o | . u4o |
| x . Q |
| | u . q | . x4o
opposite {4} |
| x . o | |
| x3x3x | x3x .
{6} first | x . x
{4} first | . x3x
{6} first |
| x3u . | u . u | . u3x |
| u3x . | x . w | . x3u |
| w . x |
x3x .
opposite {6} | u . u | . x3x
opposite {6} |
| | x . x | |
|
Lace city
in approx. ASCII-art
|
o q o
o Q o (Q=2q)
q Q Q q
o Q o
o q o
|
x
u u
x w x
x w x
u u
x
|
|
Coordinates
|
(sqrt(2), 1/sqrt(2), 0) & all permutations, all changes of sign
|
|
Volume
|
8 sqrt(2) = 11.313708
|
|
Surface
|
6+12 sqrt(3) = 26.784610
|
|
General of army
|
(is itself convex)
|
|
Colonel of regiment
|
(is itself locally convex
– no other uniform polyhedral members)
|
|
Dual
|
tekah
|
|
Dihedral angles
|
- between {4} and {6}: arccos[-1/sqrt(3)] = 125.264390°
- between {6} and {6}: arccos(-1/3) = 109.471221°
|
|
Face vector
|
24, 36, 14
|
|
Confer
|
- variations:
-
a3b3c
x3x3u
a3b4c
x3f4o
x3u4o
x3w4o
u3x4o
(-x)3x4o
- facetings:
-
tithah
pabditoe
- decompositions:
-
octatoe
- ambification:
-
retoe
- general polytopal classes:
-
Wythoffian polyhedra
lace simplices
partial Stott expansions
- analogs:
-
omnitruncated simplex otSn
truncated orthoplex tOn
bitruncated hypercube btCn
|
External
links
|






|
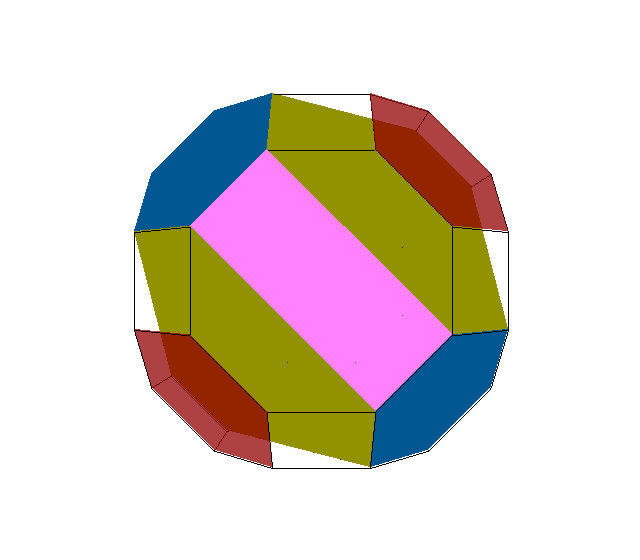
Note that toe can be thought of as the external blend of
1 oct + 8 tricues + 6 squippies,
cf. the Steward toroid K3 \ 4Q3(S3).
This decomposition is also described as the degenerate segmentochoron
xx3ox4oo&#xt.
The second picture shows how the volume of toe is intimely related to half the volume of the cube: each eighth is its vertex-first half.
Moreover it displays the interrelation between the primitve cubic and the body-centered cubic lattice, resp. their
Voronoi honeycombs each: i.e. chon and batch.
In 1887 Lord Kelvin conjectured that this tetrakaidecahedron was the best shape for packing equal-sized objects together
to fill space with minimal surface area.
But in 1994 he finally got kind of disproven, cf. Weaire, D. and Phelan, R. "A Counter-Example to Kelvin's Conjecture on Minimal Surfaces." Philos. Mag. Let. 69, 107-110, 1994.
They presented a counter-example of a space-filling geometry with even smaller surface to volume ratio,
thereby however using non-flat bounding manifolds.
Incidence matrix according to Dynkin symbol
x3x4o
. . . | 24 | 1 2 | 2 1
------+----+-------+----
x . . | 2 | 12 * | 2 0
. x . | 2 | * 24 | 1 1
------+----+-------+----
x3x . | 6 | 3 3 | 8 *
. x4o | 4 | 0 4 | * 6
snubbed forms: β3x4o, x3β4o, s3s4o (or as mere faceting qQo oqQ Qoq&#zh), β3β4o
x3x4/3o
. . . | 24 | 1 2 | 2 1
--------+----+-------+----
x . . | 2 | 12 * | 2 0
. x . | 2 | * 24 | 1 1
--------+----+-------+----
x3x . | 6 | 3 3 | 8 *
. x4/3o | 4 | 0 4 | * 6
snubbed forms: s3s4/3o
x3x3x
. . . | 24 | 1 1 1 | 1 1 1
------+----+----------+------
x . . | 2 | 12 * * | 1 1 0
. x . | 2 | * 12 * | 1 0 1
. . x | 2 | * * 12 | 0 1 1
------+----+----------+------
x3x . | 6 | 3 3 0 | 4 * *
x . x | 4 | 2 0 2 | * 6 *
. x3x | 6 | 0 3 3 | * * 4
snubbed forms: β3x3x, x3β3x, β3β3x, β3x3β, s3s3s (or as mere faceting qQo oqQ Qoq&#zh), β3β3β
s4x3x
demi( . . . ) | 24 | 1 1 1 | 1 1 1
--------------+----+----------+------
demi( . x . ) | 2 | 12 * * | 1 1 0
demi( . . x ) | 2 | * 12 * | 0 1 1
sefa( s4x . ) | 2 | * * 12 | 1 0 1
--------------+----+----------+------
s4x . ♦ 4 | 2 0 2 | 6 * *
demi( . x3x ) | 6 | 3 3 0 | * 4 *
sefa( s4x3x ) | 6 | 0 3 3 | * * 4
starting figure: x4x3x
xuxux4ooqoo&#xt → all heights = 1/sqrt(2) = 0.707107
({4} || pseudo u-{4} || pseudo (x,q)-{8} || pseudo u-{4} || {4})
o....4o.... | 4 * * * * | 2 1 0 0 0 0 0 | 1 2 0 0 0
.o...4.o... | * 4 * * * | 0 1 2 0 0 0 0 | 0 2 1 0 0
..o..4..o.. | * * 8 * * | 0 0 1 1 1 0 0 | 0 1 1 1 0
...o.4...o. | * * * 4 * | 0 0 0 0 2 1 0 | 0 0 1 2 0
....o4....o | * * * * 4 | 0 0 0 0 0 1 2 | 0 0 0 2 1
----------------+-----------+---------------+----------
x.... ..... | 2 0 0 0 0 | 4 * * * * * * | 1 1 0 0 0
oo...4oo...&#x | 1 1 0 0 0 | * 4 * * * * * | 0 2 0 0 0
.oo..4.oo..&#x | 0 1 1 0 0 | * * 8 * * * * | 0 1 1 0 0
..x.. ..... | 0 0 2 0 0 | * * * 4 * * * | 0 1 0 1 0
..oo.4..oo.&#x | 0 0 1 1 0 | * * * * 8 * * | 0 0 1 1 0
...oo4...oo&#x | 0 0 0 1 1 | * * * * * 4 * | 0 0 0 2 0
....x ..... | 0 0 0 0 2 | * * * * * * 4 | 0 0 0 1 1
----------------+-----------+---------------+----------
x....4o.... | 4 0 0 0 0 | 4 0 0 0 0 0 0 | 1 * * * *
xux.. .....&#xt | 2 2 2 0 0 | 1 2 2 1 0 0 0 | * 4 * * *
..... .oqo.&#xt | 0 1 2 1 0 | 0 0 2 0 2 0 0 | * * 4 * *
..xux .....&#xt | 0 0 2 2 2 | 0 0 0 1 2 2 1 | * * * 4 *
....x4....o | 0 0 0 0 4 | 0 0 0 0 0 0 4 | * * * * 1
or
o....4o.... & | 8 * * | 2 1 0 0 | 1 2 0
.o...4.o... & | * 8 * | 0 1 2 0 | 0 2 1
..o..4..o.. | * * 8 | 0 0 2 1 | 0 2 1
-------------------+-------+----------+------
x.... ..... & | 2 0 0 | 8 * * * | 1 1 0
oo...4oo...&#x & | 1 1 0 | * 8 * * | 0 2 0
.oo..4.oo..&#x & | 0 1 1 | * * 16 * | 0 1 1
..x.. ..... | 0 0 2 | * * * 4 | 0 2 0
-------------------+-------+----------+------
x....4o.... & | 4 0 0 | 4 0 0 0 | 2 * *
xux.. .....&#xt & | 2 2 2 | 1 2 2 1 | * 8 *
..... .oqo.&#xt | 0 2 2 | 0 0 4 0 | * * 4
xxux3xuxx&#xt → all heights = sqrt(2/3) = 0.816497
({6} || pseudo (x,u)-{6} || pseudo (u,x)-{6} || {6})
o...3o... | 6 * * * | 1 1 1 0 0 0 0 0 0 | 1 1 1 0 0 0
.o..3.o.. | * 6 * * | 0 0 1 1 1 0 0 0 0 | 0 1 1 1 0 0
..o.3..o. | * * 6 * | 0 0 0 0 1 1 1 0 0 | 0 0 1 1 1 0
...o3...o | * * * 6 | 0 0 0 0 0 0 1 1 1 | 0 0 0 1 1 1
--------------+---------+-------------------+------------
x... .... | 2 0 0 0 | 3 * * * * * * * * | 1 1 0 0 0 0
.... x... | 2 0 0 0 | * 3 * * * * * * * | 1 0 1 0 0 0
oo..3oo..&#x | 1 1 0 0 | * * 6 * * * * * * | 0 1 1 0 0 0
.x.. .... | 0 2 0 0 | * * * 3 * * * * * | 0 1 0 1 0 0
.oo.3.oo.&#x | 0 1 1 0 | * * * * 6 * * * * | 0 0 1 1 0 0
.... ..x. | 0 0 2 0 | * * * * * 3 * * * | 0 0 1 0 1 0
..oo3..oo&#x | 0 0 1 1 | * * * * * * 6 * * | 0 0 0 1 1 0
...x .... | 0 0 0 2 | * * * * * * * 3 * | 0 0 0 1 0 1
.... ...x | 0 0 0 2 | * * * * * * * * 3 | 0 0 0 0 1 1
--------------+---------+-------------------+------------
x...3x... | 6 0 0 0 | 3 3 0 0 0 0 0 0 0 | 1 * * * * *
xx.. ....&#x | 2 2 0 0 | 1 0 2 1 0 0 0 0 0 | * 3 * * * *
.... xux.&#xt | 2 2 2 0 | 0 1 2 0 2 1 0 0 0 | * * 3 * * *
.xux ....&#xt | 0 2 2 2 | 0 0 0 1 2 0 2 1 0 | * * * 3 * *
.... ..xx&#x | 0 0 2 2 | 0 0 0 0 0 1 2 0 1 | * * * * 3 *
...x3...x | 0 0 0 6 | 0 0 0 0 0 0 0 3 3 | * * * * * 1
or
o...3o... & | 12 * | 1 1 1 0 0 | 1 1 1
.o..3.o.. & | * 12 | 0 0 1 1 1 | 0 1 2
-----------------+-------+------------+------
x... .... & | 2 0 | 6 * * * * | 1 1 0
.... x... & | 2 0 | * 6 * * * | 1 0 1
oo..3oo..&#x & | 1 1 | * * 12 * * | 0 1 1
.x.. .... & | 0 2 | * * * 6 * | 0 1 1
.oo.3.oo.&#x | 0 2 | * * * * 6 | 0 0 2
-----------------+-------+------------+------
x...3x... & | 6 0 | 3 3 0 0 0 | 2 * *
xx.. ....&#x & | 2 2 | 1 0 2 1 0 | * 6 *
.... xux.&#xt & | 2 4 | 0 1 2 1 2 | * * 6
oqQ qoo4xux&#zxt → all existing heights = 0, Q = 2q = 2.828427
o.. o..4o.. | 8 * * | 1 2 0 0 | 1 2 0
.o. .o.4.o. | * 8 * | 0 2 1 0 | 1 2 0
..o ..o4..o | * * 8 | 0 0 1 2 | 0 2 1
----------------+-------+----------+------
... ... x.. | 2 0 0 | 4 * * * | 0 2 0
oo. oo.4oo.&#x | 1 1 0 | * 16 * * | 1 1 0
.oo .oo4.oo&#x | 0 1 1 | * * 8 * | 0 2 0
... ... ..x | 0 0 2 | * * * 8 | 0 1 1
----------------+-------+----------+------
oq. qo. ...&#zx | 2 2 0 | 0 4 0 0 | 4 * *
... ... xux&#xt | 2 2 2 | 1 2 2 1 | * 8 *
... ..o4..x | 0 0 4 | 0 0 0 4 | * * 2
© ©
©




