Incidence Matrices
Any polytope, honeycomb or
hyperbolic tiling is abstractly defined by its constituents (those geometric
elements of different dimensionalities) and the incidence relation thereof. Even
more general figures consisting of elements of different "dimensions"
with any correlating incidence might be tabulated in matrices.
The 0-1 Matrix of Abstract Polytopes (up)
There are different ways to list those incidences.
Often these can be found in the form of 0-1-matrices
correlating any element of "dimension" n with those of "dimension" m.
Clearly those matrices can be combined to a larger square matrix,
listing all elements of any "dimension" together with their correlating incidence.
It is convenient to provide in such a large listing groupings of the different "dimensionalities" by means of according blocks.
For instance for the tetrahedron we thus would get the matrix
v0,0,1 | 1 0 0 0 | 1 1 1 0 0 0 | 1 1 1 0
v0,0,2 | 0 1 0 0 | 1 0 0 1 1 0 | 1 1 0 1
v0,0,3 | 0 0 1 0 | 0 1 0 1 0 1 | 1 0 1 1
v0,0,4 | 0 0 0 1 | 0 0 1 0 1 1 | 0 1 1 1
------+---------+-------------+--------
e0,1,2 | 1 1 0 0 | 1 0 0 0 0 0 | 1 1 0 0
e0,1,3 | 1 0 1 0 | 0 1 0 0 0 0 | 1 0 1 0
e0,1,4 | 1 0 0 1 | 0 0 1 0 0 0 | 0 1 1 0
e0,2,3 | 0 1 1 0 | 0 0 0 1 0 0 | 1 0 0 1
e0,2,4 | 0 1 0 1 | 0 0 0 0 1 0 | 0 1 0 1
e0,3,4 | 0 0 1 1 | 0 0 0 0 0 1 | 0 0 1 1
------+---------+-------------+--------
f1,2,3 | 1 1 1 0 | 1 1 0 1 0 0 | 1 0 0 0
f1,2,4 | 1 1 0 1 | 1 0 1 0 1 0 | 0 1 0 0
f1,3,4 | 1 0 1 1 | 0 1 1 0 0 1 | 0 0 1 0
f2,3,4 | 0 1 1 1 | 0 0 0 1 1 1 | 0 0 0 1
Already this simple example displays several things.
First it shows its notational hugeness despite describing such a simple figure as the tetrahedron.
Further it is absolutely independent which geometrical representant of a tetrahedron is chosen;
special symmetrical variants (in the geometric sense) are not at all distinguished.
On the other hand this matrix is clearly symmetrical (in the matrix sense).
Thence it becomes obvious, that these incidence matrix representations are true 1:1 representations of what is known as abstract polytopes.
Symmetry Equivalence Classes of a Geometric Realization (up)
There is an other type of incidence matrices which takes account to (geometric) symmetries.
It does not list every single element on its own, it rather condenses its information by means of equivalence classes,
in fact equivalences under the action of that chosen symmetry.
It clearly is nothing but an elaboration of what once H.S.M. Coxeter intended by the term of
configuration matrix (in those days
however only being used for regular polytopes only).
Clearly geometric symmetries permute not only thus equivalent elements on their own,
but moreover permute complete flags, i.e. they maintain the local incidence relations of classes:
if e.g. a vertex is incident to a face, and this vertex is symmetry equivalent to an other vertex,
then there is a (possibly other) face incident to that other vertex, which is in the same symmetry class as the former face.
Thus that other type of incidence matrices no longer represents single elements but whole equivalence classes of symmetry,
thereby condensing multiple equivalent informations into one.
The diagonal elements thereof, instead of being just small identity matrices,
which than no longer provide any information about the total counts of the different elements,
can be exchanged by diagonal matrices giving the total counts of each equivalence class instead.
In order to show that these diagonal blocks are meant in this different sense,
the non-diagonal elements of those diagonal blocks, which have no real sense any longer, are denoted just by asterices.
To provide an example of such a compacter matrix, which shows up equivalence classes of symmetries,
here the tetrahedron (tet) is given again, but now wrt. its symmetry as a digonal antiprism:
vertices | 4 | 1 2 | 3
-------------------+---+-----+--
top- & bottom-edge | 2 | 2 * | 2
lateral edges | 2 | * 4 | 2
-------------------+---+-----+--
faces | 3 | 1 2 | 4
For other quite small and thus easy examples, showing different equivalence groupings of the same polyhedron,
look at the tetragonal pyramid (see squippy). For even simpler examples at a mere 2D level
consider the following table compiled in 2018 by Tom Ruen, showing up the different levels of symmetry being apllied:
Triangles
|
equilateral
|
isosceles
|
scalene
|
|---|
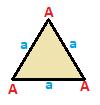
|

|

|
|
(v:3; e:3)
|
(v:2+1; e:2+1)
|
(v:1+1+1; e:1+1+1)
|
| A | a
--+---+---
A | 3 | 2
--+---+---
a | 2 | 3
|
| A B | a b
--+-----+-----
A | 2 * | 1 1
B | * 1 | 2 0
--+-----+-----
a | 1 1 | 2 *
b | 2 0 | * 1
|
| A B C | a b c
--+-------+-------
A | 1 * * | 0 1 1
B | * 1 * | 1 0 1
C | * * 1 | 1 1 0
--+-------+-------
a | 0 1 1 | 1 * *
b | 1 0 1 | * 1 *
c | 1 1 0 | * * 1
|
|
©
|
The mere incidence relations of the fully assymmetric representation are the mere 0-1-matrix again and thence a concept of abstract polytopes.
There too might be internal abstract symmetries, as is described by the automorphism group of an abstract polytope.
However the "realization" as a geometrical object is something additional.
And accordingly the (geometric) symmetries (of the specific realization that is) is on top as well.
Therefore there will be not only cases, which look different, but still describe exactly the same abstract polytope,
which then, depending on the respectively added symmetries, might or might not have the same incidence matrix of equivalence classes,
but there might occur cases as well, where non-isomorphic abstract polytopes will give rise to the same
incidence matrix of equivalence classes!
The latter occurs when incidences would become re-shuffled within the equivalence classes, e.g.
when consecutive incidences like vertex-edge incidences of non-elemental pseudo faces would close into a finite loop.
For exact incidences one always can reconstruct this very pseudo face, i.e. the length of this hole,
while when considering equivalence classes instead and multiple vertices of such a loop would happen to belong to the same class,
then the length of such a non-elemental cycle no longer would be encoded any more exactly.
This is where non-isomorphic abstract polytopes would happen to have the same incidence matrix.
Examples here would be saddid, which has such an incidence cycle of length 8,
which becomes represented in its realization as a pseudo square, and sidditdid,
which has an incidence cycle of length 12 instead, which then becomes represented in its realization as a pseudo hexagon.
In either case there are just 2 symmetry inequivalent edge types, which do alternate within these hole cycles.
Thence those no longer get differentiated, rather both polytopes will get the same incidence matrix of equivalence classes.
Non-isomorphic abstract polytopes with the same incidence matrix of symmetry classes
|
saddid
|
sidditdid
|
incidence matrix
|
|---|
 © ©
|
 © ©
|
60 | 2 2 | 1 1 2
---+-------+---------
2 | 60 * | 0 1 1
2 | * 60 | 1 0 1
---+-------+---------
3 | 0 3 | 20 * *
5 | 5 0 | * 12 *
10 | 5 5 | * * 12
|
Apart of such exeptional cases there still can be geometrically different realizations of a single abstract polytope.
And those not even are bound to respective subsymmetries only, as was examplified above in the case of the triangle (or mentioned in the squippy),
they well could occur for different realizations within the same symmetry group as well.
For instance the incidence matrix of a pentagon and a pentagram are indistinguishable. (Both consist simply of 5 vertices and 5 side elements, which are dyadically connected.)
The same
-
for o-3-o-5-x (doe) and o-3-o-5/2-x (gissid),
-
for x-3-o-5-o (ike) and x-3-o-5/2-o (gike),
-
for x-5/2-o-5-o (sissid) and x-5-o-5/2-o (gad),
-
for x-4-x-3-x (girco) and x-4/3-x-3-x (quitco),
and lots of others more.
Often these thus related (geometric) polytopes then are conjugates.
Even when this is a mere algebraical term, stemming from automorphisms of a module, in the context of polytopes this settles down to
switching between the following pairings 4/1 ↔ 4/3, 5/1 ↔ 5/3, 5/2 ↔ 5/4,
as being used as link marks in Dynkin symbols and thence happens to become a quite general concept.
This thus shows moreover, that for incidence matrices only the corresponding numerators can be relevant.
This concept of conjugation furthermore has consequences beyond the mere statistics of incidences too.
It even manifests in algebraic conjugation of values of metrical measures like the pairwise relations of vertex coordinates, of circumradii, of volumes, etc.
Some Relations (up)
Obviously those symmetry respecting incidence matrices are no longer bound to be symmetrical.
But still there is some kind of intercorrelation of numbers which nearly halves the effort (just as for 0-1-matrices).
If Ii,j is the matrix element of the i-th row and the j-th column, we have the equation
Ii,i * Ii,j = Ij,i * Ij,j
This relation is true, independent to whether the corresponding boundaries are incident or not;
for in the latter case the non-diagonal elements will be both zero.
Further, for the diagonal elements clearly the Euler equation (possibly with genus or other extension) holds.
The same for all subdiagonal elements of each row (the subpolytopes),
and alike for all super-diagonal elements of each row (the figures of complementary space to each kind of subpolytope,
such as vertex figures, edge figures, etc.).
Even the group order can be read from the (second kind of) incidence matrices.
Choose any element of the last diagonal block (some facet count),
multiply it with some facet count of the corresponding (n-1)-subpolytope,
multiply that by some facet count of the corresponding (n-2)-subpolytope,
and so on until you end in a vertex-edge incidence number.
In fact this is because that is nothing but a way of counting the flags.
For n=2 this is depicted below:
. . . | . . . | . . .
. . . | . . . | . . .
. . . | . . . | . . .
---------+----------+---------
. . . | . . . | . . .
. I0,1 .<--. . . | . . .
. . . | . ^ . | . . .
---------+----|-----+---------
. . . | . . . | . . .
. . . | . I1,2 .<--. I2,2 .
. . . | . . . | . . .
I0,1 * I1,2 * I2,2 = g
Reading an incidence diagram (Hasse diagram) of an abstract polytope top-down,
one gets the incidence diagram of the dual abstract polytope.
That is, (n-k-1)-subploytopes correspond to k-subpolytopes of the dual polytope.
But again this is a feature of the flag:
if a set of subpolytopial elements of different dimensionalities is mutually incident,
then the set of piecewise dual elements is mutually incident too.
Because dualization not only is a mere abstract polytopal concept,
but well could be described as a geometric construction device too (at least as long as all elements remain within finite reach,
or by considering projective space instead) it becomes clear that dualization will respect symmetry equivalences as well.
Therefore even the incidence matrices (by symmetry equivalence) of any abstract polytope should be quite nicely correlated to the one of its dual partner.
Indeed, just turn the matrix by 180 degrees:
tesseract (tes) <-dual-> hexadecachoron (hex)
16 | 4 | 6 | 4 8 | 6 | 12 | 8
---+----+----+-- --+----+----+---
2 | 32 | 3 | 3 ,--> 2 | 24 | 4 | 4
---+----+----+-- |180°| --+----+----+---
4 | 4 | 24 | 2 <--' 3 | 3 | 32 | 2
---+----+----+-- --+----+----+---
8 | 12 | 6 | 8 4 | 6 | 4 | 16
If we would restrict to polytopes with a linear Dynkin diagram, that is to polytopes with
Schläfli symbol {a,b,...,c,d},
where a, b, ..., c, d are the rational subdivisors of π of the angles between the corresponding mirrors,
together with all their truncates, i.e. the polytopes tw,x,...,y,z{a,b,...,c,d},
then further relations can be deduced, correlating the incidence matrix numbers for the different truncates.
So consider in the following any arbitrary group [a,b,...,c,d] to be fixed, and abreviate the truncates just
by their truncation-prefix. Then we have the following relations:
The number of vertices of a truncated polytope, I0,0(tw,x,...,y,z),
is related to the matrix entries of the untruncated one, Ii,j(t0), by
I0,0(tw,x,...,y,z) = Iz,z(t0) * Iz,y(t0) *...* Ix,w(t0).
The number of a given type of edges of a polytope having a certain truncated Schläfli symbol is identical with the number
of vertices of that polytope which has its vertices at the center of edges of the former.
The Dynkin diagram of the latter has all the nodes of the former ringed,
plus the neighbouring nodes of that node corresponding to the edge under consideration, minus that single node.
Hence, f.i. for polychora
I1,1(t1,3,4)|1 = I0,0(t0,2,3,4),
I1,1(t1,3,4)|3 = I0,0(t1,2,4),
I1,1(t1,3,4)|4 = I0,0(t1,3).
The number of a given type of a higher dimensional boundary of a polytope having a certain truncated Schläfli symbol
finally is identical with the number of vertices of that polytope which has its vertices at the center of those boundaries.
Using a kind of iteration of the former, getting nothing but an infinitely iterated projection of the
Wythoff point
into the related hyperplanes, one comes up with the final truncated Schläfli symbol (Dynkin diagram) of the second polytope.
It has all nodes of the former ringed, plus the neighbours of those nodes which correspond to the Dynkin diagram of the boundary,
minus those nodes of the boundary itself. Hence, f.i. for polychora
I2,2(t1,4)|0,1 = I0,0(t2,4),
I2,2(t1,4)|1,2 = I0,0(t0,3,4),
I2,2(t1,4)|1,4 = I0,0(t0,2,3),
I2,2(t1,4)|3,4 = I0,0(t1,2).
The set of uniform polytopes also is easily recognizable from their incidence matrices.
Those necessarily ask for n0 = 1, i.e. use only a single class of symmetry-equivalent vertices.
(In fact, this latter restriction equates to what is called isogonality. The further restriction
to unit-sized edge lengths only would not be transported into the incidence matrix numbers for sure.)
–
Likewise any noble polytope can be easily translated into incidence matrix restrictions:
There we ought to have n0 = nD-1 = 1, i.e. with only a single class of symmetry-equivalent vertices
and additionally a single class of symmetry-equivalent facets.
–
Regular polytopes finally clearly would require to have nk = 1
for any subdimension k.
But note however that the converse would not be true:
e.g. in the rhombic tiling all dimensional elements are equivalent each,
but the flags (incidence structures of vertex, edge, face, ...) still fall into 2 different classes
of acute and obtuse corners.
Incidence Matrices for Compounds
Like polytopes of one dimension above, compounds use several polytopes of that base dimension.
Accordingly their incidence matrix too will no longer show up the base-dimensional polytopes, i.e. the component polytopes,
within the diagonal (which is reserved for the overall counts), but will have to add to the matrix an additional row-block
for those, displaying the count of the individual component at the final, i.e. diagonal block element,
so that it would look more like a matrix for a polytope of one dimension above.
None the less, if base-dimension is n, although having n+1 blocks, the (individual) row-sum within the
block element, positioned at the intersection of the nth block-column and (n-1)st block-row,
still equals 2 (according to the Euler relation). – In comparision to (normal) polytopes of one dimension above, the same relation
would be asked nominally for the block with the same description as just given, but there we would have to replace n
by n+1 as well (as being one dimension above), so that in consequence this condition would take place within a different
block! (Even though, in order to better distinguish these types of matrices visually, the new added block-column will be separated by a
double stroke, cf. the example given below.)
The row-sum of the entries of the last block-column usually will be 1, except for the final one, which clearly counts the
components. This is true as long all elements, whether completely coincident or not, are counted separately. If, for
instance, the vertices fall together pairwise, then surely they could be chosen to be identified as well. In consequence the formerly
individual vertex figures will become compounds in turn. Thereby the individual vertex count is divided by some number, the coincidence count (here by 2),
while all other numbers of this very row will be multiplied by the same number. This matrix transformation still fulfills
the matrix relation cited in chapter Some Relations above. Thereby too the entries of the last block-column
will be multiplied. Thus those show up, in this case, the number of components of the vertex figure compound.
To provide an example, we look at rhom, the compound of 5 cubes
within a doe. (Note the vertex figure numbers "6" in the right matrix below:
Those describe a (non-regular) compound of 2 triangles, kind of a mutually rotated star of David.)
coincident vertices,
taken separately: being identified:
40 | 3 | 3 || 1 20 | 6 | 6 || 2
---+----+----++-- ---+----+----++--
2 | 60 | 2 || 1 2 | 60 | 2 || 1
---+----+----++-- ---+----+----++--
4 | 4 | 30 || 1 4 | 4 | 30 || 1
---+----+----++-- ---+----+----++--
8 | 12 | 6 || 5 8 | 12 | 6 || 5
As can be seen already in that single example: the vertex figure element counts are no longer the full super-diagonal parts
of the rows of the first row-block, instead they have to be terminated before the additional last column-block (i.e. the double-stroke).
The same holds true for the edge figures etc. Alternatively one could consider that additional elements as body counts of the corresponding
dimensionality. – Seen in that view, even incidence matrices of "normal" polytopes could be given that same extension
of the last row and column; just that all entries of the last column there would be 1, and the non-diagonal elements of the
last row would copy the number of the corresponding diagonal element. (In fact, this trivial form of those is why they will not be
used for "normal" polytopes.)
Strictly speaking, only those figures, with a non-unit number within the final block (at the lower left end) and
with all other final entries being 1, can be called true compounds. All other cases would already step somehow
towards the mere (single) polytope by means of the applied unifications, as those vertex identifications (or more
generally: combinations of several individual elements to a single sub-dimensional compound figure) would interlink
the formerly still separate components. Also the entries of the lowest block-row (the components) strictly would be
wrong, as those clearly use individual elements instead of combined ones. - None the less, they will be given
here, within that extended incidence matrix notation, for completeness too.
Note:
Be aware of the ♦-sign used sometimes within the incidence matrices given for higherdimensional polytopes.
Those are links to the incidence matrices of the corresponding sub-polytope, possibly its vertex figure etc.
(Btw., the inverse mapping, listing the larger polytopes, where some given polytope is a facet of, is provided
as separate "used as facet" page. A further similar inverse mapping is accessible as separate
"used as vertex figure" page too.)




