 ©
©
| Site Map | Polytopes | Dynkin Diagrams | Vertex Figures, etc. | Incidence Matrices | Index |
This is the title of a famous book of H.S.M. Coxeter, and accordingly lots of the following can be found there too. (The below provided tables by dimensions had been assembled by D. de Winters, but his webpage ceased to exist after his death. They are thus reproduced here, in a further enriched form.)
The high degree of symmetry of regular polytopes induces lots of inter-relations onto the set of regular polytopes. There are not only dual pairings (which, according to regularity, both have to be regular polytopes!), but even the set of vertices (up to radial scalings) often are commonly used for large subsets each. Polytopes can be grouped accordingly to the dimensional size of shared sub-elements. The following systematics of Olshevsky does not only apply to regulars, but for the above reasons clearly has lots of applications here:
| shared sub-elements |
name of group | most convex representant |
|---|---|---|
| 0 | army | general |
| 1 | regiment | colonel |
| 2 | company | captain |
| n | n-regiment | n-colonel |
In more detail, the army general of some regular (or even uniform) polytope always is its convex hull. Conversely, that polytope is a (full symmetrical) faceting of its army general. Alike, any polytope can be considered as an edge faceting of its regiment colonel, i.e. a faceting which respects the given edge skeleton. Thereby its vertex figure obviously belongs to the army of the vertex figure of its colonel. Note that this does not imply the other way round, that the colonel always will have a convex vertex figure (which also is known as local convexity of the polytope itself). Sure, most often it does, but there will be cases, where a coating of the edge skeleton in the sense of a convex vertex figure, demanded from one end of the edges, would ask for additional edges at the opposite end, which do not belong to the actual edge skeleton. Then the colonel would be chosen as the one with a vertex figure being as convex as possible. For instance this takes place for the 10-tet-compound (e), where there are only 2 provided edges within each potential locally coating face plane.
(Johnson extended this nomenclatura slightly, by calling 2 or more different regiments (of the same army), using the same edge length, a brigade. Further, a subset of polytopes of a brigade, which is closed under the operation of blending, is called a cohort. – Even close relatives of colonels deserve a special name, attributed by Bowers: lieutenants he calls the conjugates of colonels, which not themselves are colonels.)
Compounds too can fall into the same army as some regular polytope. This is what Coxeter once called vertex regularity.
Just as the chords of polygons are defined as its vertex-to-vertex line-segments, generally any polytope shows up similarily chords of different lengths. Those might be grouped into ones of the same size, and further the classes might be ordered (and thereby named) by increasing size. A 0-chord then would be the vertex adjoined to itself, and for uniform convex polytopes the 1-chords would be the set of edges.
In the following, compounds (esp. the polygonal ones), if not stated otherwise, are understood to be (fully) regular ones.
---- 2D ----
| army general |
vertex count |
chord number |
edge count |
scaling factor |
(unscaled) regiment colonel |
|---|---|---|---|---|---|
| {3} = x3o | 3 | 1st | 3 | x | {3} = x3o |
| {4} = x4o | 4 | 1st | 4 | x | {4} = x4o |
| {5} = x5o | 5 | 1st | 5 | x | {5} = x5o |
| 2nd | 5 | f | {5/2} = x5/2o | ||
| {6} = x6o | 6 | 1st | 6 | x | {6} = x6o |
| 2nd | 6 | h | 2-x3o-compound (star of David) = {6}[2{3}]{6} |
||
| {7} = x7o | 7 | 1st | 7 | x | {7} = x7o |
| 2nd | 7 | x(7) | {7/2} = x7/2o | ||
| 3rd | 7 | x(7,3) = 1/[1-1/x(7)] |
{7/3} = x7/3o | ||
| {8} = x8o | 8 | 1st | 8 | x | {8} = x8o |
| 2nd | 8 | x(8) | 2-x4o-compound = {8}[2{4}]{8} |
||
| 3rd | 8 | w = 1+q |
{8/3} = x8/3o | ||
| {9} = x9o | 9 | 1st | 9 | x | {9} = x9o |
| 2nd | 9 | x(9) | {9/2} = x9/2o | ||
| 3rd | 9 | x(9,3) = 2+1/x(9) |
3-x3o-compound = {9}[3{3}]{9} |
||
| 4th | 9 | x(9,4) = 1+x(9) |
{9/4} = x9/4o | ||
| {10} = x10o | 10 | 1st | 10 | x | {10} = x10o |
| 2nd | 10 | x(10) | 2-x5o-compound = {10}[2{5}]{10} |
||
| 3rd | 10 | x(10,3) = f f = 1+f |
{10/3} = x10/3o | ||
| 4th | 10 | x(10,4) = f x(10) |
2-x5/2o-compound = {10}[2{5/2}]{10} |
||
| etc. | |||||
---- 3D ----
| army general |
vertex count |
chord number |
edge count |
scaling factor |
(unscaled) regiment colonel |
(unscaled) faceting face |
face count |
(unscaled) company captain |
|---|---|---|---|---|---|---|---|---|
| tet | 4 | 1st | 6 | x | tet | x3o | 4 | tet = {3,3} = x3o3o |
| oct | 6 | 1st | 12 | x | oct | x3o | 8 | oct = {3,4} = x3o4o |
| x4o | 3 | – | ||||||
| cube | 8 | 1st | 12 | x | cube | x4o | 6 | cube = {4,3} = x4o3o |
| 2nd | 12 | q | so | x3o | 8 | so (stella octangula) = 2-tet-compound = {4,3}[2{3,3}]{3,4} |
||
| ike | 12 | 1st | 30 | x | ike | x3o | 20 | ike = {3,5} = x3o5o |
| x5o | 12 | gad = {5,5/2} = x5o5/2o | ||||||
| 2nd | 60 | f | sissid | x5/2o | 12 | sissid = {5/2,5} = x5/2o5o | ||
| x3o | 20 | gike = {3,5/2} = x3o5/2o | ||||||
| doe | 20 | 1st | 30 | x | doe | x5o | 12 | doe = {5,3} = x5o3o |
| 2nd | 60 | f | (sidtid) | x5/2o | 12 | – | ||
| x3o | 20 | – | ||||||
| x4o | 30 | rhom = 5-cube-compound = 2{5,3}[5{4,3}] |
||||||
| x5o | 12 | – | ||||||
| 3rd | 60 | f q | e | non-regular 2-x3o-compound |
20 | e = 10-tet-compound = 2{5,3}[10{3,3}]2{3,5} |
||
| 4th | 30 | f f | gissid | x5/2o | 12 | gissid = {5/2,3} = x5/2o3o |
©
---- 4D ----
| army general |
vertex count |
chord number |
edge count |
scaling factor |
(unscaled) regiment colonel |
(unscaled) faceting face |
face count |
(unscaled) company captain |
(unscaled) faceting cell |
cell count |
(unscaled) 3-regiment 3-colonel |
|---|---|---|---|---|---|---|---|---|---|---|---|
| pen | 5 | 1st | 10 | x | pen | x3o | 10 | pen | tet | 5 | pen = {3,3,3} = x3o3o3o |
| hex | 8 | 1st | 24 | x | hex | x3o | 32 | hex | tet | 16 | hex = {3,3,4} = x3o3o4o |
| oct | 4 | – | |||||||||
| x4o | 6 | – | |||||||||
| tes | 16 | 1st | 32 | x | tes | x4o | 24 | tes | cube | 8 | tes = {4,3,3} = x4o3o3o |
| 2nd | 48 | q | haddet | x3o | 64 | haddet | tet | 32 | haddet = 2-hex-compound = {4,3,3}[2{3,3,4}] |
||
| oct | 8 | – | |||||||||
| x4o | 12 | – | |||||||||
| 3rd | 32 | h | – | ||||||||
| ico | 24 | 1st | 96 | x | ico | x3o | 96 | ico | oct | 24 | ico = {3,4,3} = x3o4o3o |
| x4o | 72 | gico | cube | 24 | gico = 3-tes-compound = 2{3,4,3}[3{4,3,3}]{3,4,3} |
||||||
| x6o | 16 | – | |||||||||
| 2nd | 72 | q | sico | x3o | 96 | sico | so | 24 | sico = 3-hex-compound = {3,4,3}[3{3,3,4}]2{3,4,3} |
||
| oct | 12 | – | |||||||||
| x4o | 18 | – | |||||||||
| 3rd | 96 | h | – | 2-x3o- compound = {6}[2{3}]{6} |
16 | – | |||||
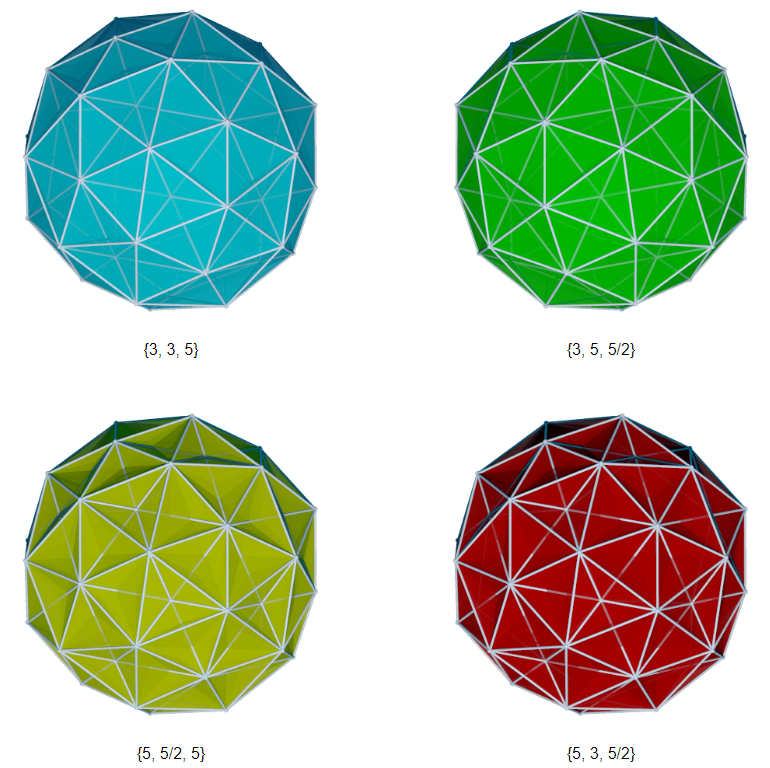
| ex | 120 | 1st | 720 | x | ex | x3o | 1200 | ex | tet | 600 | ex = {3,3,5} = x3o3o5o |
| ike | 120 | fix = {3,5,5/2} = x3o5o5/2o | |||||||||
| x5o | 720 | gahi | doe | 120 | gahi = {5,3,5/2} = x5o3o5/2o | ||||||
| gad | 120 | gohi = {5,5/2,5} = x5o5/2o5o | |||||||||
| x10o | 72 | – | |||||||||
| 2nd | 1200 | f | sishi | x5/2o | 720 | sishi | sissid | 120 | sishi = {5/2,5,3} = x5/2o5o3o | ||
| x3o | 2400 | dox | gike | 120 | – | ||||||
| tet | 600 | – | |||||||||
| oct | 600 | dox = 25-ico-compound = 5-chi-compound = 5{3,3,5}[25{3,4,3}]{3,3,5} |
|||||||||
| ike | 120 | – | |||||||||
| x4o | 1800 | dac | cube | 600 | dac = 75-tes-compound = 25-gico-compound = 10{3,3,5}[75{4,3,3}]5{5,3,3} |
||||||
| x5o | 720 | gaghi | gad | 120 | gaghi = {5,5/2,3} = x5o5/2o3o | ||||||
| x6o | 200 | – | |||||||||
| 3rd | 720 | x(10) | – | 2-x5o- compound = {10}[2{5}]{10} |
72 | – | |||||
| 4th | 1800 | f q | [75hex] | x3o | 2400 | [75hex] | tet | 1200 | [75hex] = 75-hex-compound = 25-sico-compound = 5{3,3,5}[75{3,3,4}]10{5,3,3} |
||
| oct | 300 | – | |||||||||
| x4o | 450 | – | |||||||||
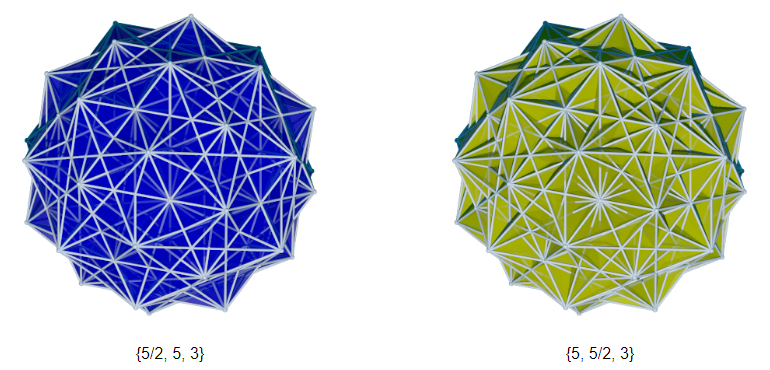
| 5th | 720 | f f | gishi | x5/2o | 720 | gishi | gissid | 120 | gishi = {5/2,3,5} = x5/2o3o5o | ||
| sissid | 120 | gashi = {5/2,5,5/2} = x5/2o5o5/2o | |||||||||
| x3o | 1200 | gofix | gike | 120 | gofix = {3,5/2,5} = x3o5/2o5o | ||||||
| tet | 600 | gax = {3,3,5/2} = x3o3o5/2o | |||||||||
| x10/3o | 72 | – | |||||||||
| 6th | 1200 | f u | – | 2-x3o- compound = {6}[2{3}]{6} |
200 | – | |||||
| 7th | 720 | f x(10) | – | 2-x5/2o- compound = {10}[2{5/2}]{10} |
72 | – | |||||
| hi | 600 | 1st | 1200 | x | hi | x5o | 720 | hi | doe | 120 | hi = {5,3,3} = x5o3o3o |
| 2nd | 3600 | f | (sidtaxhi) | x5/2o | 720 | – | |||||
| x3o | 2400 | – | tet | 600 | – | ||||||
| x4o | 3600 | – | cube | 600 | – | ||||||
| x5o | 1440 | – | doe | 120 | – | ||||||
| x10o | 720 | – | |||||||||
| 3rd | 7200 | f q | sody | x3o | 12000 | sody | tet | 6000 | sody = 10-ex-compound = 2{5,3,3}[10{3,3,5}] |
||
| ike | 1200 | fassody = 10-fix-compound = 2{5,3,3}[10{3,5,5/2}]2{3,3,5} |
|||||||||
| x5o | 7200 | godex | gad | 1200 | godex = 10-gohi-compound = 2{5,3,3}[10{5,5/2,5}]2{3,3,5} |
||||||
| doe | 1200 | gadex = 10-gahi-compound = 2{5,3,3}[10{5,3,5/2}]2{3,3,5} |
|||||||||
| x10o | 720 | – | |||||||||
| 4th | 3600 | f f | (dattady) | x5/2o | 1440 | – | gissid | 120 | – | ||
| x3o | 1200 | – | |||||||||
| x4o | 3600 | – | cube | 600 | – | ||||||
| x5o | 1440 | – | doe | 120 | – | ||||||
| x6o | 1200 | – | |||||||||
| 5th | 1200 | f h | – | ||||||||
| 6th | 7200 | f x(10) | – | 2-x5/2o- compound = {10}[2{5/2}]{10} |
720 | – | |||||
| x4o | 3600 | – | |||||||||
| 7th | 7200 | [?] | – | x5o | 1440 | – | |||||
| 8th | 9600 | f f q | sisdex | x5/2o | 7200 | sisdex | sissid | 1200 | sisdex = 10-sishi-compound = 2{5,3,3}[10{5/2,5,3}]2{3,3,5} |
||
| x3o | 21600 | [225ico] | gike | 1200 | – | ||||||
| tet | 6000 | – | |||||||||
| oct | 5400 | [225ico] = 225-ico-compound = 9{5,3,3}[225{3,4,3}] |
|||||||||
| ike | 1200 | – | |||||||||
| x4o | 16200 | [675tes] | cube | 5400 | [675tes] = 675-tes-compound = 18{5,3,3}[675{4,3,3}]9{3,3,5} |
||||||
| x5o | 7200 | gigadex | gad | 1200 | gigadex = 10-gaghi-compound = 2{5,3,3}[10{5,5/2,3}]2{3,3,5} |
||||||
| x6o | 1600 | – | |||||||||
| 9th | 7200 | [?] | – | x5o | 1440 | – | |||||
| 10th | 3600 | f f f | (gadtaxady) | x5/2o | 720 | – | gissid | 120 | – | ||
| x3o | 2400 | – | tet | 600 | – | ||||||
| x10/3o | 720 | – | |||||||||
| x4o | 3600 | – | cube | 600 | – | ||||||
| x5o | 720 | – | |||||||||
| 11th | 7200 | f q x(10) | – | 2-x5o- compound = {10}[2{5}]{10} |
720 | – | |||||
| 12ath | 7200 | f f h | – | 2-x3o- compound = {6}[2{3}]{6} |
1200 | – | |||||
| x4o | 3600 | – | |||||||||
| 12bth | 1200 | – | |||||||||
| 13th | 7200 | [?] | – | x3o | 2400 | – | |||||
| 14th | 7200 | f f x(10) | – | 2-x5/2o- compound = {10}[2{5/2}]{10} |
720 | – | |||||
| x4o | 3600 | – | |||||||||
| 15th | 16200 | f f u | [675hex] | x3o | 21600 | [675hex] | tet | 10800 | [675hex] = 675-hex-compound = 9{5,3,3}[675{4,3,3}]18{3,3,5} |
||
| oct | 2700 | – | |||||||||
| x4o | 4050 | – | |||||||||
| 16th | 7200 | [?] | – | ||||||||
| 17th | 7200 | [?] | – | x5/2o | 1440 | – | |||||
| 18ath | 7200 | f (2+f) = f f sqrt(5) |
[720pen] | x3o | 7200 | [720pen] | tet | 3600 | [720pen] = 720-pen-compound = 6{5,3,3}[720{3,3,3}] |
||
| 18bth | 1200 | mix | x3o | 1200 | mix | tet | 600 | mix = 120-pen-compound = {5,3,3}[120{3,3,3}]{3,3,5} |
|||
| 19th | 7200 | f f f q | gisdex | x5/2o | 7200 | gisdex | gissid | 6000 | gisdex = 10-gishi-compound = 2{5,3,3}[10{5/2,3,5}]2{3,3,5} |
||
| sissid | 1200 | gasdex = 10-gashi-compound = 2{5,3,3}[10{5/2,5,5/2}]2{3,3,5} |
|||||||||
| x3o | 12000 | gifsody | gike | 1200 | gifsody = 10-gofix-compound = 2{5,3,3}[10{3,5/2,5}]2{3,3,5} |
||||||
| tet | 6000 | gassody = 10-gax-compound = 2{5,3,3}[10{3,3,5/2}] |
|||||||||
| x10/3o | 720 | – | |||||||||
| 20th | 3600 | [?] | – | ||||||||
| 21st | 7200 | [?] | – | x3o | 2400 | – | |||||
| 22nd | 9600 | f f q h | – | 2-x3o- compound = {6}[2{3}]{6} |
1600 | – | |||||
| 23rd | 7200 | [?] | – | x5/2o | 1440 | – | |||||
| 24th | 7200 | [?] | – | ||||||||
| 25th | 1200 | f f f f | gogishi | x5/2o | 720 | gogishi | gissid | 120 | gogishi = {5/2,3,3} = x5/2o3o3o | ||
| 26th | 3600 | [?] | – | ||||||||
| 27th | 7200 | f f q x(10) | – | 2-x5/2o- compound = {10}[2{5/2}]{10} |
720 | – | |||||
| 28th | 3600 | [?] | – | ||||||||
| 29th | 1200 | f f f h | – | ||||||||
| 1st : ex, fix, gohi, gahi | 2nd : sishi, gaghi | 5th : gax, gofix, gashi, gishi |
|---|---|---|
|
|

|
© 2004-2024 | top of page |