Acronym	...
Name	complex polyhedron sp-4-o2-3-o2, (γp3)/p
Circumradius	sqrt(3/8) / sin(π/p)
Coordinates	(εpn, εpm, εpk)/(sqrt(8) sin(π/p))   for any 1≤n,m,k≤p, where εp=exp(2πi/p) and n+m+k ≡ 0 mod(p)
Face vector	p2, 3p2, p(p+3)
Confer	general polytopal classes: complex polytopes
External links

This is the snub when being applied onto x_p-4-o₂-3-o₂, the coordinates of which there had been given as (ε_pⁿ, ε_p^m, ε_p^k)/(2 sin(π/p)) for any 1≤n,m,k≤p, where ε_p=exp(2πi/p). Here now the pre-image of the s_p node consists of a p-edge. None the less an according alternation is still possible, but then it is no longer one out of two, rather it is selecting (locally!) one out of p instead. In fact, this afore mentioned quest amounts in a further relation on those possible exponents of the coordinates: n+m+k ≡ 0 mod(p).

The former vertex figure, coming in as full-dimensional sectioning facets underneath, as such firstly have the former vertex count. However, like the vertices themselves, these too fall into p modulo classes, i.e. forming a compound. Just a single thereof will be supported by the selected vertices. Thence the count of those sefas is 1/p of the former vertex count.

Besides those sefas, here there will be the further polygons s_p-4-o₂ as well, which come in as subdimensional snubs of the facets of the pre-image. The total edge count could be derived from the edge count per vertex. To that purpose one observes that the new vertex-incident edges here just are aligned as diagonals of the vertex-incident squares of the real hypercube, the pre-image is a generalizing of. Thus this number generally is given simply as 2 choose(D, 2), where D is the according dimensionality of that real space hypercube. Alternatively it turns out to be derivable simply as the total edge count of those s_p-4-o₂ faces.

As usual with snubs, the scaling wrt. the pre-image is to be chosen independly. In here the just existing 2-edges are those which matter and get sized to unity. This choice then provides the above given metrical properties.

It shall be noted, that this snub, as given below, happens to result in a fully dyadic configuration again after all. This even is true for any value of p, but for p>2 it is to be embedded into 3-dimensional complex space or equivalently into 6-dimensional real space. Complex polytopes on the other hand do not require dyadicity at all. Thus additional faces, having the same set of supporting "edges" might come in freely. E.g. for p=3 this would allow for a set of further 9 triangles: This then is what C.G. Shephard means when stating (γ³₃)/3 = β³₃, which indeed has the same 9 vertices, the same 27 edges, but then rather uses 27 instead of just 18 triangular faces.

In fact, it even is that "almost regular" complex polyhedron, which C.G. Shephard and H.S.M. Coxeter denoted respectively by:

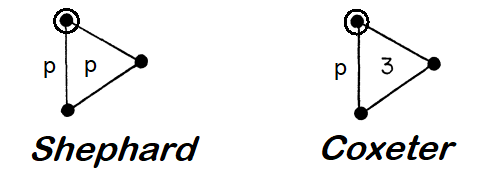
where Coxeter refers by that "almost regularity" to this complex "non-closing" behaviour within 3-dimensional space, or to higher-dimensional polytopes, which do implement such a 3-dimensional one.

Incidence matrix according to Dynkin symbol

sp-4-o2-3-o2

p-th( .    .    .  ) | p2 |  6  |  3 3 
--------------------+----+-----+------
edge( sp-4-o2   .  ) | 2  | 3p2 |  1 1 
--------------------+----+-----+------
      sp-4-o2   .    ♦ p  |  p  | 3p * 
sefa( sp-4-o2-3-o2 ) | 3  |  3  |  * p2

starting figure: xp-4-o2-3-o2