|
Acronym
|
tuta (alt.: pabdirit, tutcup, tutaltut), tut || inv tut, K-4.55
|
|
Name
|
truncated tetrahedral alterprism,
truncated tetrahedral cupoliprism,
runcic snub cubic hosochoron,
truncated tetrahedron atop inverted truncated tetrahedron,
truncated tetrahedron atop alternate truncated tetrahedron,
tetrahedrally medial part of rectified tesseract,
parabidiminished rectified tesseract
|
Segmentochoron display /
VRML
|
⭳
|
|
Cross sections
|
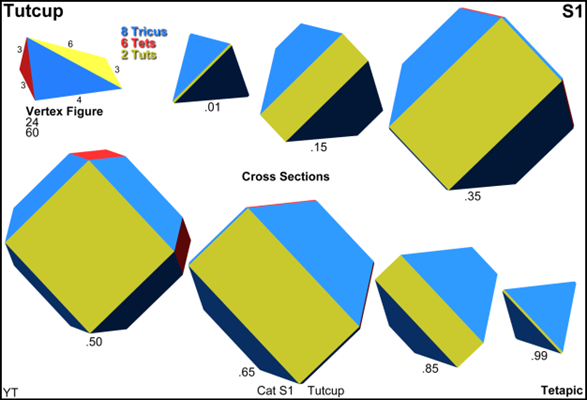 © ©
|
|
Circumradius
|
sqrt(3/2) = 1.224745
|
Lace city
in approx. ASCII-art
|
x3x o3x
u3o o3u
x3o x3x
|
|
Coordinates
|
(3, 1, 1, 1)/sqrt(8) all permutations in first 3 coords, even changes of sign in all coords
|
|
General of army
|
(is itself convex)
|
|
Colonel of regiment
|
(is itself locally convex)
|
|
Dihedral angles
|
|
|
Face vector
|
24, 60, 52, 16
|
|
Confer
|
- uniform relative:
-
rit
- segmentochora:
-
tet || tut
- related CRFs:
-
mibdirit
- general polytopal classes:
-
scaliform
segmentochora
lace simplices
|
External
links
|




|
This polychoron also can be derived as equatorial stratos of rit, if that one will be considered with respect to an axial
tetrahedral symmetry.
Klitzing in automn of 2000 both found this very polychoron and also obtained therefrom the precise concept of some weakening of uniformity, which
shortly thereafter became known as scaliformity. Thus tutcup truely was the first known scaliform polytope!
Incidence matrix according to Dynkin symbol
xo3xx3ox&#x → height = 1/sqrt(2) = 0.707107
(tut || inv tut)
o.3o.3o. | 12 * | 1 2 2 0 0 | 2 1 2 2 1 0 0 | 1 2 1 1 0
.o3.o3.o | * 12 | 0 0 2 2 1 | 0 0 1 2 2 1 2 | 0 1 1 2 1
------------+-------+--------------+------------------+----------
x. .. .. | 2 0 | 6 * * * * | 2 0 2 0 0 0 0 | 1 2 1 0 0
.. x. .. | 2 0 | * 12 * * * | 1 1 0 1 0 0 0 | 1 1 0 0 0
oo3oo3oo&#x | 1 1 | * * 24 * * | 0 0 1 1 1 0 0 | 0 1 1 1 0
.. .x .. | 0 2 | * * * 12 * | 0 0 0 1 0 1 1 | 0 1 0 1 1
.. .. .x | 0 2 | * * * * 6 | 0 0 0 0 2 0 2 | 0 0 1 2 1
------------+-------+--------------+------------------+----------
x.3x. ..&#x | 6 0 | 3 3 0 0 0 | 4 * * * * * * | 1 1 0 0 0
.. x.3o. | 3 0 | 0 3 0 0 0 | * 4 * * * * * | 1 0 0 1 0
xo .. ..&#x | 2 1 | 1 0 2 0 0 | * * 12 * * * * | 0 1 1 0 0
.. xx ..&#x | 2 2 | 0 1 2 1 0 | * * * 12 * * * | 0 1 0 1 0
.. .. ox&#x | 1 2 | 0 0 2 0 1 | * * * * 12 * * | 0 0 1 1 0
.o3.x .. | 0 3 | 0 0 0 3 0 | * * * * * 4 * | 0 1 0 0 1
.. .x3.x&#x | 0 6 | 0 0 0 3 3 | * * * * * * 4 | 0 0 0 1 1
------------+-------+--------------+------------------+----------
x.3x.3o. ♦ 12 0 | 6 12 0 0 0 | 4 4 0 0 0 0 0 | 1 * * * *
xo3xx ..&#x ♦ 6 3 | 3 3 6 3 0 | 1 0 3 3 0 1 0 | * 4 * * *
xo .. ox&#x ♦ 2 2 | 1 0 4 0 1 | 0 0 2 0 2 0 0 | * * 6 * *
.. xx3ox&#x ♦ 3 6 | 0 3 6 3 3 | 0 1 0 3 3 0 1 | * * * 4 *
.o3.x3.x ♦ 0 12 | 0 0 0 12 6 | 0 0 0 0 0 4 4 | * * * * 1
or
o.3o.3o. & | 24 | 1 2 2 | 2 1 3 2 | 1 3 1
--------------+----+----------+-----------+------
x. .. .. & | 2 | 12 * * | 0 0 2 0 | 1 2 1
.. x. .. & | 2 | * 24 * | 1 1 0 1 | 1 2 0
oo3oo3oo&#x | 2 | * * 24 | 0 0 2 1 | 0 2 1
--------------+----+----------+-----------+------
x.3x. ..&#x & | 6 | 3 3 0 | 8 * * * | 1 1 0
.. x.3o. & | 3 | 0 3 0 | * 8 * * | 1 1 0
xo .. ..&#x & | 3 | 1 0 2 | * * 24 * | 0 1 1
.. xx ..&#x | 4 | 0 2 2 | * * * 12 | 0 2 0
--------------+----+----------+-----------+------
x.3x.3o. & ♦ 12 | 6 12 0 | 4 4 0 0 | 2 * *
xo3xx ..&#x & ♦ 9 | 3 6 6 | 3 1 3 3 | * 8 *
xo .. ox&#x ♦ 4 | 2 0 4 | 0 0 4 0 | * * 6
s4o3x2s
demi( . . . . ) | 24 | 2 1 2 | 1 2 2 3 | 1 1 3
----------------+----+----------+-----------+------
demi( . . x . ) | 2 | 24 * * | 1 1 1 0 | 1 0 2
s4o . . | 2 | * 12 * | 0 0 2 2 | 1 1 2
s . 2 s | 2 | * * 24 | 0 1 0 2 | 0 1 2
----------------+----+----------+-----------+------
demi( . o3x . ) | 3 | 3 0 0 | 8 * * * | 1 0 1
s 2 x2s | 4 | 2 0 2 | * 12 * * | 0 0 2
sefa( s4o3x . ) | 6 | 3 3 0 | * * 8 * | 1 0 1
sefa( s4o 2 s ) | 3 | 0 1 2 | * * * 24 | 0 1 1
----------------+----+----------+-----------+------
s4o3x . ♦ 12 | 12 6 0 | 4 0 4 0 | 2 * *
s4o 2 s ♦ 4 | 0 2 4 | 0 0 0 4 | * 6 *
sefa( s4o3x2s ) ♦ 9 | 6 3 6 | 1 3 1 3 | * * 8
starting figure: x4o3x x
©


