Home

Equilateral Strictly-Convex Polyhedra with Polytiles

There are 92 Johnson solids, strictly convex equilateral polyhedra made from regular polygon faces. There has so far been no serious effort to try to enumerate convex equilateral polyhedra made from polytile faces.

Such equilateral polyhedra, might be called polytilehedra  or p-tilehedra in general. And within a specific p-tile, the number strictly convex polyhedra is finite. There's no need to limit faces to a single p-set, but if a polyhedron is made from p-tiles and q-tiles, they can be considered as r-tiles where r=pq/gcd(p,q).

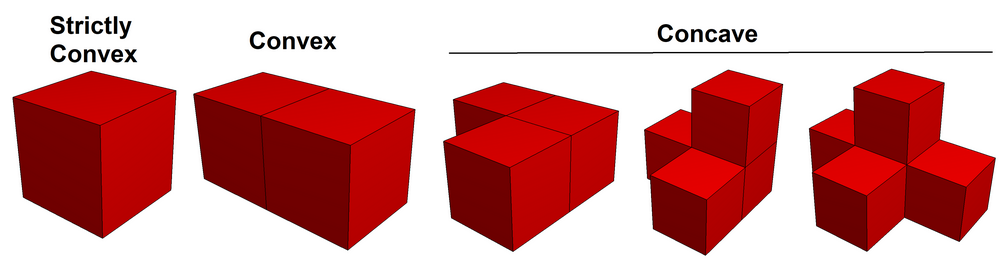
Tetratilehedra (cubes)

The simplest examples are topological cubes, with square faces. The only convex tetratilehedron is a cube, since the only strictly convex tetratile is a square. (Other tetratilehedra can be constructed as face-to-face cubes, or polycubes, like examples shown)

Rhombohedra (rhombic-faced)

The same topology of a cube exist with rhombi faces, trigonal trapezohedra if all rhombs are identical, and most generally rhombohedra, with 3 pairs of identical rhombi. Zonohedra are made from all rhombic faces, so they could also be p-tilehedra.

Equilateral parallelohedra (hexagon and rhombic)

A parallelohedron is one of 5 topologies: cube, hexagonal prism, rhombic dodecahedron, elongated dodecahedron, and truncated octahedron, made from rhombic and hexagonal or parallelogon faces, having central symmetry. Edges can be but are not required to be equilateral.

Prisms

© 2020-2021 Created by Tom Ruen