Acronym	...
Name	Powertope {p}{8}
	© (Note that for the herein being called length-factor w in the picture the letter q is being used instead.)
Circumradius	sqrt[1+1/sqrt(2)]/sin(π/p)
Especially	p y circumradius 3 2/sqrt(3) = 1.154701 sqrt[(4+2 sqrt(2))/3] = 1.508689 4 sqrt(2) = 1.414214 sqrt[2+sqrt(2)] = 1.847759 5 sqrt[(10+2 sqrt(5))/5] = 1.701302 sqrt[(20+10 sqrt(2)+4 sqrt(5)+2 sqrt(10))/10] = 2.222858 6 2 sqrt[4+2 sqrt(2)] = 2.613126 8 sqrt[4+2 sqrt(2)] = 2.613126 2+sqrt(2) = 3.141214
Confer	general polytopal classes: isogonal
External links

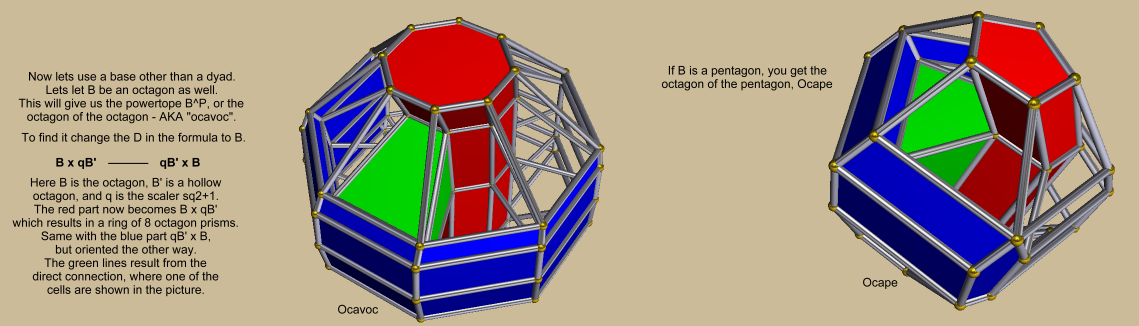
The Powertope asks here to use the p-fold ring of the (long) prisms x.-p-o. w. .. from the first layer plus the orthogonal p-fold ring of (long) prisms .w .. .x-p-.o from the other layer, and then to connect them directly, i.e. in a lacing sense. These lacing elements thus are rectangular trapezoprisms where the rectangular bases have edge sizes x and w, while the lacing edge size will be y, as is just described by the elements xw .. wx ..&#zy.

Incidence matrix according to Dynkin symbol

xw-p-oo wx-p-oo&#zy   where: w = 1+sqrt(2) = 2.414214
                             y = 1/sin(π/p)

o.-p-o. o.-p-o.    & | 2pp |   2   2  1 |  1   4   4 |  2  4
---------------------+-----+------------+------------+------
x.   .. ..   ..    & |   2 | 2pp   *  * |  1   2   1 |  2  2
..   .. w.   ..    & |   2 |   * 2pp  * |  0   2   1 |  1  2
..   .. ..   ..&#y   |   2 |   *   * pp |  0   0   4 |  0  4
---------------------+-----+------------+------------+------
x.-p-o. ..   ..    & |   p |   p   0  0 | 2p   *   * |  2  0
x.   .. w.   ..    & |   4 |   2   2  0 |  * 2pp   * |  1  1
xw   .. ..   ..&#y & |   4 |   1   1  2 |  *   * 2pp |  0  2
---------------------+-----+------------+------------+------
x.-p-o. w.   ..    & ♦  2p |  2p   p  0 |  2   p   0 | 2p  *
xw   .. wx   ..&#y   ♦   8 |   4   4  4 |  0   2   4 |  * pp