Abstract Polytopes
B. Grünbaum in 1977 found some special abstract polytope which since then is known as 11-cell.
H.S.M. Coxeter in 1982 came up with a related figure, the 57-cell.
- What is special about these figures?
- How are they "constructed"?
- Are there other relatives?
The essential of the construction of these abstract polytopes needs some side step first.
This one leads from spherical space to elliptical space.
Spherical spaces are those of the surface of a ball of any dimension.
Elliptical spaces are locally the same ones, even adopting the corresponding metrics,
but do identify every pair of opposite points.
Esp. the last of the above questions drove Coxeter to look way beyond this special setup too.
Together with W.O.J. Moser he looked for so called regular maps in toroidal spaces.
Together with J.F. Petrie he even earlier looked for skew polyhedra.
The polytopes of elliptical space (up)
-
Any convex polytope of any dimension can be projected from its center onto some circumscribing sphere of according dimension.
This derives some spherical tesselation from the polytope.
-
If the polytope did have point symmetry with respect to its center, the tesselation too will have.
In these cases those spherical tesselations would lead to corresponding elliptical tesselations,
right by identification of opposite points.
All polytopes with inversion symmetry therefore will lead to some elliptical polytopes, here-below denoted
by a leading lower case letter e as operant for the elliptical space counterpart (e(...)).
As an aside, if the polytope did not have point symmetry with respect to its center, one might consider the compound with its inverse as starting figure instead.
Then the same construction described above again applies. For sure, by the indentification of antipodes the incidence structure of the
elliptical space outcome then does not differ from that of the single starting polytope, and therefore is not considered a truely
new structure here. Thus we might simply identify e.g. e(xo3oo3ox) = e(x3o3o + o3o3x) with x3o3o
(although they clearly live in different spaces). And note, that in elliptical space the realization still requires the local double cover of the spherical space
compound!
As these again are abstract polytopes, one could thus speak of elliptical polytopes as well.
Elliptical polytopes can alternatively be considered as polytopes of projective space.
For regular polytopes (of normal spherical space) the equatorial zig-zag is the according Petrie polygon.
The identification of pairs of antipodal points, when proceding from spherical to elliptical space, thus reduces the length H of that skew polygon likewise to its half.
Just as the regular polytopes of spherical space often are provided by their Schläfli symbol {P,Q,...,R} instead of their equivalent
Coxeter diagram xPoQo...oRo, and, if aiming to stress the length of its Petrie polygon additionally, sometimes even are denoted as
{P,Q,...,R}H, then the regular elliptical polytopes e(xPoQo...oRo) sometimes become denoted alternatively
as {P,Q,...,R}H/2. (Note that H/2 clearly is integral here due to the overall restriction to centrically symmetric polytopes.)
The following listing is not ment to be complete. They only show the general procedures,
and will be given explicitly whenever they will be used for the Grünbaum-Coxeter polytopes below.
e(x-2n-o) (n>1)
{2n}n
hemi-2n-gon
|
hemi(. .) | n | 2
----------+---+--
hemi(x .) | 2 | n
| | |
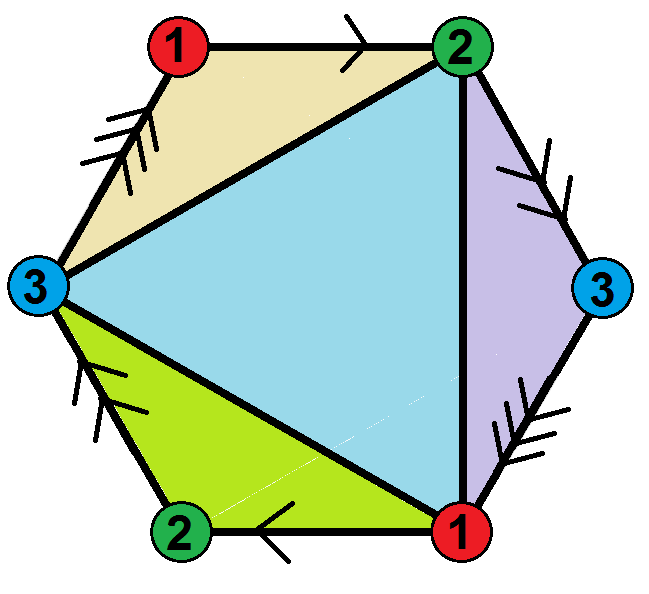
e(x3o4o)
{3,4}3
elloct
hemi-octahedron
 © ©
|
hemi(. . .) | 3 | 4 | 4
------------+---+---+--
hemi(x . .) | 2 | 6 | 2
------------+---+---+--
hemi(x3o .) | 3 | 3 | 4
|
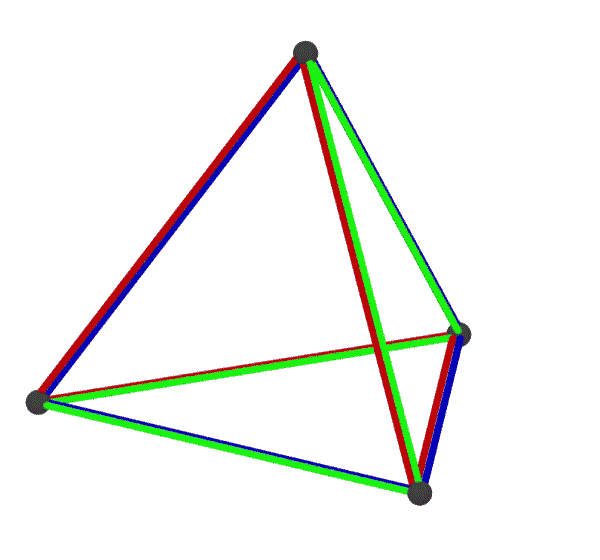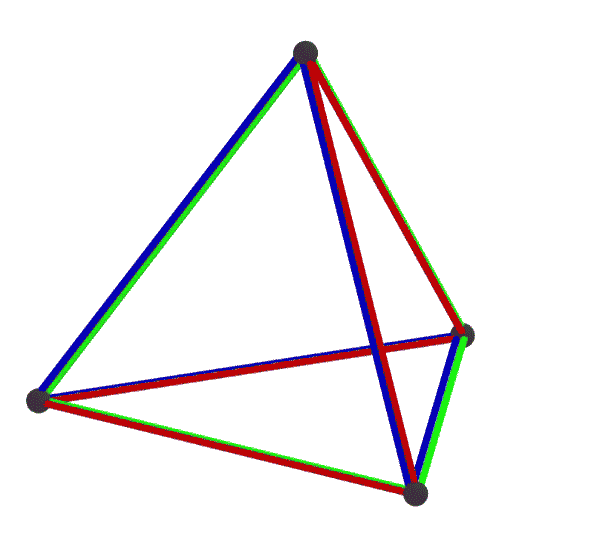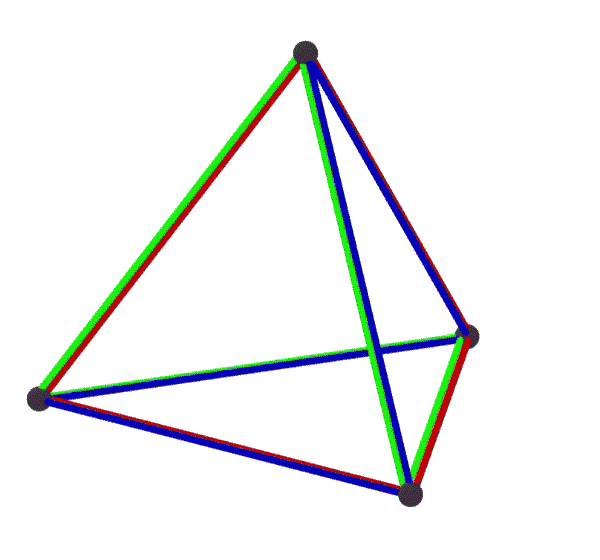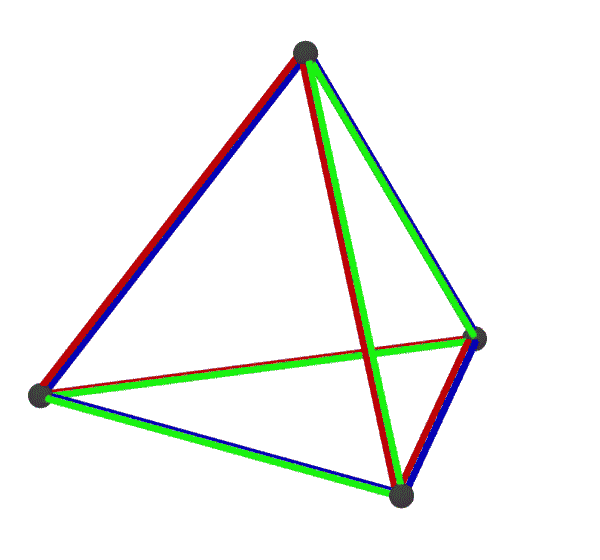
e(x4o3o)
{4,3}3
elcube
hemi-cube
 © ©
 © ©
|
hemi(. . .) | 4 | 3 | 3
------------+---+---+--
hemi(x . .) | 2 | 6 | 2
------------+---+---+--
hemi(x4o .) | 4 | 4 | 3
|
e(o3x4o)
elco
hemi-cuboctahedron
|
hemi(. . .) | 6 | 4 | 2 2
------------+---+----+----
hemi(. x .) | 2 | 12 | 1 1
------------+---+----+----
hemi(o3x .) | 3 | 3 | 4 *
hemi(. x4o) | 4 | 4 | * 3
| | |
e(x3x4o)
eltoe
truncated hemi-octahedron
|
hemi(. . .) | 12 | 1 2 | 2 1
------------+----+------+----
hemi(x . .) | 2 | 6 * | 2 0
hemi(. x .) | 2 | * 12 | 1 1
------------+----+------+----
hemi(x3x .) | 6 | 3 3 | 4 *
hemi(. x4o) | 4 | 0 4 | * 3
|
e(o3x4x)
eltic
truncated hemi-cube
|
hemi(. . .) | 12 | 2 1 | 1 2
------------+----+------+----
hemi(. x .) | 2 | 12 * | 1 1
hemi(. . x) | 2 | * 6 | 0 2
------------+----+------+----
hemi(o3x .) | 3 | 3 0 | 4 *
hemi(. x4x) | 8 | 4 4 | * 3
|
e(x3o4x)
elsirco
small rhombated hemi-cuboctahedron
(more general:
e(y3o4x) with "y" = x,q,f,...)
|
hemi(. . .) | 12 | 2 2 | 1 2 1
------------+----+-------+------
hemi(x . .) | 2 | 12 * | 1 1 0
hemi(. . x) | 2 | * 12 | 0 1 1
------------+----+-------+------
hemi(x3o .) | 3 | 3 0 | 4 * *
hemi(x . x) | 4 | 2 2 | * 6 *
hemi(. o4x) | 4 | 0 4 | * * 3
|
e(x3x4x)
elgirco
great rhombated hemi-cuboctahedron
|
hemi(. . .) | 24 | 1 1 1 | 1 1 1
------------+----+----------+------
hemi(x . .) | 2 | 12 * * | 1 1 0
hemi(. x .) | 2 | * 12 * | 1 0 1
hemi(. . x) | 2 | * * 12 | 0 1 1
------------+----+----------+------
hemi(x3x .) | 6 | 3 3 0 | 4 * *
hemi(x . x) | 4 | 2 0 2 | * 6 *
hemi(. x4x) | 8 | 0 4 4 | * * 3
|
e(x3o5o)
{3,5}5
ellike
hemi-icosahedron
 © ©
|
hemi(. . .) | 6 | 5 | 5
------------+---+----+---
hemi(x . .) | 2 | 15 | 2
------------+---+----+---
hemi(x3o .) | 3 | 3 | 10
|
e(x5o3o)
{5,3}5
eldoe
hemi-dodecahedron
 © ©
 © ©
|
hemi(. . .) | 10 | 3 | 3
------------+----+----+--
hemi(x . .) | 2 | 15 | 2
------------+----+----+--
hemi(x5o .) | 5 | 5 | 6
|
As an aside:
The edge graph of ellike also is known as K6,
the complete graph with 6 vertices.
|
As a further aside:
The edge graph of eldoe also is known as
the Peterson graph (given in the right pic above).
|
e(o3x5o)
ellid
hemi-icosidodecahedron
|
hemi(. . .) | 15 | 4 | 2 2
------------+----+----+-----
hemi(. x .) | 2 | 30 | 1 1
------------+----+----+-----
hemi(o3x .) | 3 | 3 | 10 *
hemi(. x5o) | 5 | 5 | * 6
| | |
e(x3x5o)
elti
truncated hemi-icosahedron
|
hemi(. . .) | 30 | 1 2 | 2 1
------------+----+-------+-----
hemi(x . .) | 2 | 15 * | 2 0
hemi(. x .) | 2 | * 30 | 1 1
------------+----+-------+-----
hemi(x3x .) | 6 | 3 3 | 10 *
hemi(. x5o) | 5 | 0 5 | * 6
|
e(o3x5x)
eltid
truncated hemi-dodecahedron
|
hemi(. . .) | 30 | 2 1 | 1 2
------------+----+-------+-----
hemi(. x .) | 2 | 30 * | 1 1
hemi(. . x) | 2 | * 15 | 0 2
------------+----+-------+-----
hemi(o3x .) | 3 | 3 0 | 10 *
hemi(. x5x) | 10 | 5 5 | * 6
|
e(x3o5x)
elsrid
small rhombated hemi-icosidodecahedron
(more general:
e(y3o5x) with "y" = x,q,f,...)
|
hemi(. . .) | 30 | 2 2 | 1 2 1
------------+----+-------+--------
hemi(x . .) | 2 | 30 * | 1 1 0
hemi(. . x) | 2 | * 30 | 0 1 1
------------+----+-------+--------
hemi(x3o .) | 3 | 3 0 | 10 * *
hemi(x . x) | 4 | 2 2 | * 15 *
hemi(. o5x) | 5 | 0 5 | * * 6
|
e(x3x5x)
elgrid
great rhombated hemi-icosidodecahedron
|
hemi(. . .) | 60 | 1 1 1 | 1 1 1
------------+----+----------+--------
hemi(x . .) | 2 | 30 * * | 1 1 0
hemi(. x .) | 2 | * 30 * | 1 0 1
hemi(. . x) | 2 | * * 30 | 0 1 1
------------+----+----------+--------
hemi(x3x .) | 6 | 3 3 0 | 10 * *
hemi(x . x) | 4 | 2 0 2 | * 15 *
hemi(. x5x) | 10 | 0 5 5 | * * 6
|
e(x3o3o4o)
{3,3,4}4
elhex
hemi-hexadecachoron
|
hemi(. . . .) | 4 ♦ 6 | 12 | 8
--------------+---+----+----+--
hemi(x . . .) | 2 | 12 | 4 | 4
--------------+---+----+----+--
hemi(x3o . .) | 3 | 3 | 16 | 2
--------------+---+----+----+--
hemi(x3o3o .) ♦ 4 | 6 | 4 | 8
|
e(x4o3o3o)
{4,3,3}4
eltes
hemi-tesseract
|
hemi(. . . .) | 8 ♦ 4 | 6 | 4
--------------+---+----+----+--
hemi(x . . .) | 2 | 16 | 3 | 3
--------------+---+----+----+--
hemi(x4o . .) | 4 | 4 | 12 | 2
--------------+---+----+----+--
hemi(x4o3o .) ♦ 8 | 12 | 6 | 4
|
e(o3x3o4o)
ellico
hemi-icositetrachoron
|
hemi(. . . .) | 12 ♦ 8 | 4 8 | 4 2
--------------+----+----+-------+----
hemi(. x . .) | 2 | 48 | 1 2 | 2 1
--------------+----+----+-------+----
hemi(o3x . .) | 3 | 3 | 16 * | 2 0
hemi(. x3o .) | 3 | 3 | * 32 | 1 1
--------------+----+----+-------+----
hemi(o3x3o .) ♦ 6 | 12 | 4 4 | 8 *
hemi(. x3o4o) ♦ 6 | 12 | 0 8 | * 4
| | |
e(x3o4o3o)
{3,4,3}6
ellico
hemi-icositetrachoron
|
hemi(. . . .) | 12 ♦ 8 | 12 | 6
--------------+----+----+----+---
hemi(x . . .) | 2 | 48 | 3 | 3
--------------+----+----+----+---
hemi(x3o . .) | 3 | 3 | 48 | 2
--------------+----+----+----+---
hemi(x3o4o .) ♦ 6 | 12 | 8 | 12
| | |
e(x3o3o5o)
{3,3,5}15
ellex
hemi-hexacosachoron
|
hemi(. . . .) | 60 ♦ 12 | 30 | 20
--------------+----+-----+-----+----
hemi(x . . .) | 2 | 360 | 5 | 5
--------------+----+-----+-----+----
hemi(x3o . .) | 3 | 3 | 600 | 2
--------------+----+-----+-----+----
hemi(x3o3o .) ♦ 4 | 6 | 4 | 300
|
e(x5o3o3o)
{5,3,3}15
elhi
hemi-hecatonicosachoron
Davis manifold
|
hemi(. . . .) | 300 ♦ 4 | 6 | 4
--------------+-----+-----+-----+---
hemi(x . . .) | 2 | 600 | 3 | 3
--------------+-----+-----+-----+---
hemi(x5o . .) | 5 | 5 | 360 | 2
--------------+-----+-----+-----+---
hemi(x5o3o .) ♦ 20 | 30 | 12 | 60
|
e(o3x3x3o)
eldeca
hemi-decachoron
|
hemi(. . . .) | 15 | 4 | 2 4 | 4
----------------+----+----+-------+--
hemi(. x . .) & | 2 | 30 | 1 2 | 3
----------------+----+----+-------+--
hemi(o3x . .) & | 3 | 3 | 10 * | 2
hemi(. x3x .) | 6 | 6 | * 10 | 2
----------------+----+----+-------+--
hemi(o3x3x .) & ♦ 12 | 18 | 4 4 | 5
|
e(o3x4x3o)
elcont
hemi-tetracontoctachoron
|
hemi(. . . .) | 144 | 4 | 2 4 | 4
----------------+-----+-----+-------+---
hemi(. x . .) & | 2 | 288 | 1 2 | 3
----------------+-----+-----+-------+---
hemi(o3x . .) & | 3 | 3 | 96 * | 2
hemi(. x4x .) | 8 | 8 | * 72 | 2
----------------+-----+-----+-------+---
hemi(o3x4x .) & ♦ 24 | 36 | 8 6 | 24
|
e(x3o3o3x)
elspid
hemi-small-prismated-decachoron
|
hemi(. . . .) | 10 | 6 | 6 6 | 2 6
----------------+----+----+-------+-----
hemi(x . . .) & | 2 | 30 | 2 2 | 1 3
----------------+----+----+-------+-----
hemi(x3o . .) & | 3 | 3 | 20 * | 1 1
hemi(x . . x) | 4 | 4 | * 15 | 0 2
----------------+----+----+-------+-----
hemi(x3o3o .) & ♦ 4 | 6 | 4 0 | 5 *
hemi(x3o . x) & ♦ 6 | 9 | 2 3 | * 10
|
e(x3o4o3x)
elspic
hemi-small-prismated-icositetrachoron
|
hemi(. . . .) | 72 | 8 | 8 8 | 2 8
----------------+----+-----+---------+------
hemi(x . . .) & | 2 | 288 | 2 2 | 1 3
----------------+----+-----+---------+------
hemi(x3o . .) & | 3 | 3 | 192 * | 1 1
hemi(x . . x) | 4 | 4 | * 144 | 0 2
----------------+----+-----+---------+------
hemi(x3o4o .) & ♦ 6 | 12 | 8 0 | 24 *
hemi(x3o . x) & ♦ 6 | 9 | 2 3 | * 96
|
e(x x3o4o)
ellope
hemi - octahedron-prism
|
hemi(. . . .) | 6 | 1 4 | 4 4 | 4 1
--------------+---+------+-----+----
hemi(x . . .) | 2 | 3 * | 4 0 | 4 0
hemi(. x . .) | 2 | * 12 | 1 2 | 2 1
--------------+---+------+-----+----
hemi(x x . .) | 4 | 2 2 | 6 * | 2 0
hemi(. x3o .) | 3 | 0 3 | * 8 | 1 1
--------------+---+------+-----+----
hemi(x x3o .) ♦ 6 | 3 6 | 3 2 | 4 *
hemi(. x3o4o) ♦ 6 | 0 12 | 0 8 | * 1
|
e(x x4o3o)
eltes
hemi-tesseract
|
hemi(. . . .) | 8 ♦ 1 3 | 3 3 | 3 1
--------------+---+------+-----+----
hemi(x . . .) | 2 | 4 * | 3 0 | 3 0
hemi(. x . .) | 2 | * 12 | 1 2 | 2 1
--------------+---+------+-----+----
hemi(x x . .) | 4 | 2 2 | 6 * | 2 0
hemi(. x4o .) | 4 | 0 4 | * 6 | 1 1
--------------+---+------+-----+----
hemi(x x4o .) ♦ 8 | 4 8 | 4 2 | 3 *
hemi(. x4o3o) ♦ 8 | 0 12 | 0 6 | * 1
|
e(x4o x4o)
eltes
hemi-tesseract
|
hemi(. . . .) | 8 ♦ 2 2 | 1 4 1 | 2 2
--------------+---+-----+-------+----
hemi(x . . .) | 2 | 8 * | 1 2 0 | 2 1
hemi(. . x .) | 2 | * 8 | 0 2 1 | 1 2
--------------+---+-----+-------+----
hemi(x4o . .) | 4 | 4 0 | 2 * * | 2 0
hemi(x . x .) | 4 | 2 2 | * 8 * | 1 1
hemi(. . x4o) | 4 | 0 4 | * * 2 | 0 2
--------------+---+-----+-------+----
hemi(x4o x .) ♦ 8 | 8 4 | 2 4 0 | 2 *
hemi(x . x4o) ♦ 8 | 4 8 | 0 4 2 | * 2
| | |
e(x3o3o3o4o)
{3,3,3,4}5
eltac
hemi-triacontiditeron
|
hemi(. . . . .) | 5 ♦ 8 | 24 | 32 | 16
----------------+---+----+----+----+---
hemi(x . . . .) | 2 | 20 ♦ 6 | 12 | 8
----------------+---+----+----+----+---
hemi(x3o . . .) | 3 | 3 | 40 | 4 | 4
----------------+---+----+----+----+---
hemi(x3o3o . .) ♦ 4 | 6 | 4 | 40 | 2
----------------+---+----+----+----+---
hemi(x3o3o3o .) ♦ 5 | 10 | 10 | 5 | 16
|
e(x4o3o3o3o)
{4,3,3,3}5
elpent
hemi-penteract
|
hemi(. . . . .) | 16 ♦ 5 | 10 | 10 | 5
----------------+----+----+----+----+--
hemi(x . . . .) | 2 | 40 ♦ 4 | 6 | 4
----------------+----+----+----+----+--
hemi(x4o . . .) | 4 | 4 | 40 | 3 | 3
----------------+----+----+----+----+--
hemi(x4o3o . .) ♦ 8 | 12 | 6 | 20 | 2
----------------+----+----+----+----+--
hemi(x4o3o3o .) ♦ 16 | 32 | 24 | 8 | 5
|
e(o3x3o3o4o)
elrat
rectified hemi-triacontiditeron
|
hemi(. . . . .) | 20 ♦ 12 | 6 24 | 12 16 | 8 2
----------------+----+-----+--------+-------+-----
hemi(. x . . .) | 2 | 120 | 1 4 | 4 4 | 4 1
----------------+----+-----+--------+-------+-----
hemi(o3x . . .) | 3 | 3 | 40 * | 4 0 | 4 0
hemi(. x3o . .) | 3 | 3 | * 160 | 1 2 | 2 1
----------------+----+-----+--------+-------+-----
hemi(o3x3o . .) ♦ 6 | 12 | 4 4 | 40 * | 2 0
hemi(. x3o3o .) ♦ 4 | 6 | 0 4 | * 80 | 1 1
----------------+----+-----+--------+-------+-----
hemi(o3x3o3o .) ♦ 10 | 30 | 10 20 | 5 5 | 16 *
hemi(. x3o3o4o) ♦ 8 | 24 | 0 32 | 0 16 | * 5
|
e(o3o3x3o4o)
elnit
hemi-penteractitriacontiditeron
|
hemi(. . . . .) | 40 ♦ 12 | 12 12 | 4 12 3 | 4 3
----------------+----+-----+---------+----------+-----
hemi(. . x . .) | 2 | 240 | 2 2 | 1 4 1 | 2 2
----------------+----+-----+---------+----------+-----
hemi(. o3x . .) | 3 | 3 | 160 * | 1 2 0 | 2 1
hemi(. . x3o .) | 3 | 3 | * 160 | 0 2 1 | 1 2
----------------+----+-----+---------+----------+-----
hemi(o3o3x . .) ♦ 4 | 6 | 4 0 | 40 * * | 2 0
hemi(. o3x3o .) ♦ 6 | 12 | 4 4 | * 80 * | 1 1
hemi(. . x3o4o) ♦ 6 | 12 | 0 8 | * * 20 | 0 2
----------------+----+-----+---------+----------+-----
hemi(o3o3x3o .) ♦ 10 | 30 | 20 10 | 5 5 0 | 16 *
hemi(. o3x3o4o) ♦ 24 | 96 | 32 64 | 0 16 8 | * 5
|
e(x4o x3o4o)
elsquoct
hemi - square-octahedron-duoprism
|
hemi(. . . . .) | 12 | 2 4 | 1 8 4 | 4 8 1 | 4 2
----------------+----+-------+---------+--------+----
hemi(x . . . .) | 2 | 12 * | 1 4 0 | 4 4 0 | 4 1
hemi(. . x . .) | 2 | * 24 | 0 2 2 | 1 4 1 | 2 2
----------------+----+-------+---------+--------+----
hemi(x4o . . .) | 4 | 4 0 | 3 * * | 4 0 0 | 4 0
hemi(x . x . .) | 4 | 2 2 | * 24 * | 1 2 0 | 2 1
hemi(. . x3o .) | 3 | 0 3 | * * 16 | 0 2 1 | 1 2
----------------+----+-------+---------+--------+----
hemi(x4o x . .) ♦ 8 | 8 4 | 2 4 0 | 6 * * | 2 0
hemi(x . x3o .) ♦ 6 | 3 6 | 0 3 2 | * 16 * | 1 1
hemi(. . x3o4o) ♦ 6 | 0 12 | 0 0 8 | * * 2 | 0 2
----------------+----+-------+---------+--------+----
hemi(x4o x3o .) ♦ 12 | 12 12 | 3 12 4 | 3 4 0 | 4 *
hemi(x . x3o4o) ♦ 12 | 6 24 | 0 12 16 | 0 8 2 | * 2
| | |
Note that a thing like e(o3x3o) could not exist, as it uses the tetrahedral subsymmetry of the oct,
so that the diametral identification does not apply - or rather would reproduce the full symmetry again. (For sure e(x3o4o) clearly does exist.)
On the other hand e(o3x3o4o) does exist indeed, as here the hexic subsymmetry of the ico is being
emphasized, which itself shows up the inversion element already.
In the same run e(o3x3x3o) and e(x3o3o3x) would not exist in the stronger sense, simply because the emphasized pennic symmetry does not
contain the inversion element. But when looking at those polychora in the higher decaic symmetry, then they become allowed again,
i.e. eldeca and elspid exist non the same.
But, as in this special cases there isn't a different representation for these views, it gets maintained here as such. It is only that in those cases the additional
summing in the matrices (cf. "&") becomes crucial in these cases.
(The similar pairing of icoic and contic symmetry does not show up this problem,
as clearly both provide the inversion element themselves.)
The construction of Grünbaum-Coxeter polytopes (up)
Essentially Grünbaum-Coxeter polytopes are set up like usual polytopes.
But instead of usual spherical space polytopes for facets, they use elliptical space ones.
And additionally instead of spherical space polytopes for vertex figures, they use elliptical space ones.
Instead of this bottom-up construction by doing elliptical identifications of elements first
and then adding small things to larger structures in whatever spaces
these thingies might live in, also a top-down construction can be applied.
One could well start with usual (regular) tesselations {p, q, ..., r}, and apply kind
of modulo-wrappings to them in order to derive GC{p, q, ..., r} by identifications of elements.
Kind of like this has been done according to the cellular and vertex figural identifications of opposite incident elements.
|
|
.png)
|
|
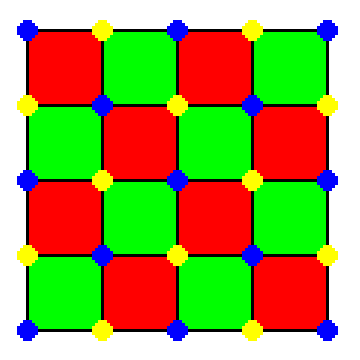
GC(x4o4o) as mod-wrapp of x4o4o
|
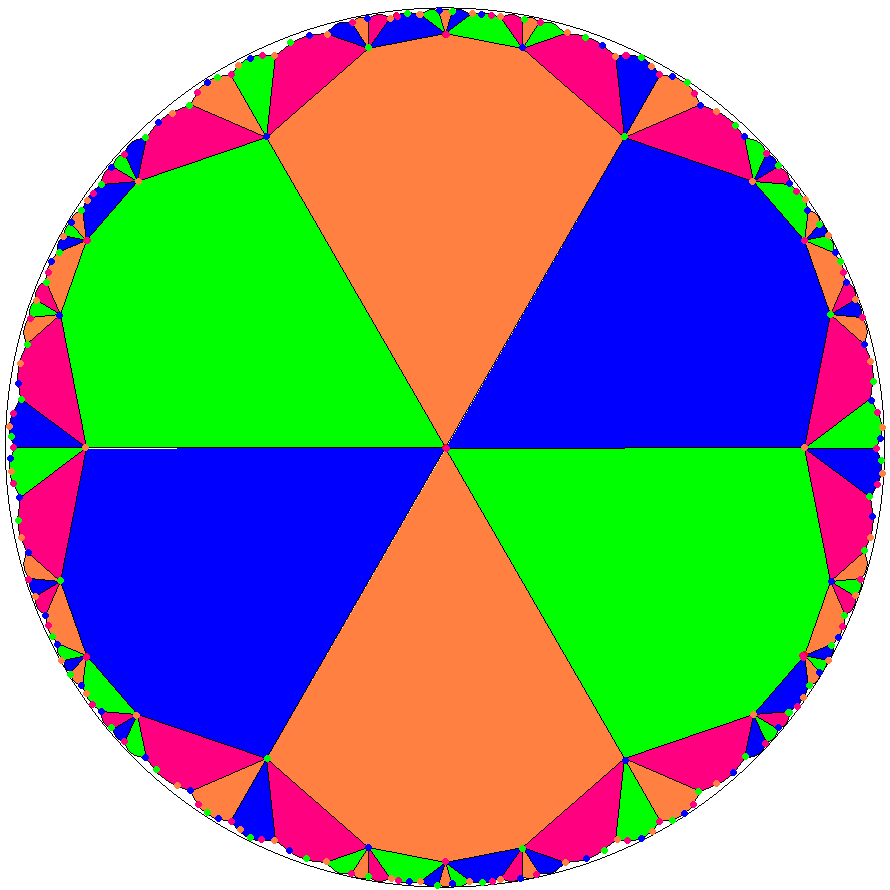
GC(x6o6o) as mod-wrapp of x6o6o
|
GC(x4o4o6*a) as mod-wrapp of x4o4o6*a
|
Surprisingly it comes out in 3D that there is some general isomorphism between
GC(x-2N-o-2M-o) and x-N-o-M-o,
as can be seen from the incidence matrices shown below.
–
This can be understood as follows.
The face polygons of GC(x-2N-o-2M-o) are e(x-2N-o .), which virtually
function like x-N-o. On the other hand the vertex figure of GC(x-2N-o-2M-o)
is (up to scaling) e(. x-2M-o), which in turn virtually functions like x-M-o.
Those two objects interlink mutually and will produce (bottom-up) finally the logical structure of x-N-o-M-o.
The same holds true for the closed loop Dynkin symbols of that dimension, i.e. for GC(x-2P-o-2Q-o-2R-*a).
Here the faces are e(x-2P-o . ) and e(x . o-2R-*a),
which virtually function like x-P-o resp. x-R-o. The vertex figure of
GC(x-2P-o-2Q-o-2R-*a) is e(. a-2Q-b ), where the edge sizes
a and b depend on 2P resp. 2R and additionally on the elliptical
identification of these faces.
The final functionality of that vertex figure is like x(P)-Q-x(R).
Therefore GC(x-2P-o-2Q-o-2R-*a) comes out to be isomorphic to x-P-o-Q-o-R-*a.
(It should be noted, that here either of P, Q, R might be 2 as well, but that the reduction
of these digons is not allowed, cf. digons within abstract polytopes.)
- *)
-
In cases denoted by this asterisk, the pre-images of the facets under the identifications (top-down method)
are cells of the respective tiling, which are monostratic only, i.e. have vertices in exactly 2 parallel layers.
Therefore the identification will pass on the vertex numbers of the cellular top-facet to the bottom-facet,
and all cellular latteral facets too do have the same numbered vertices.
Accodingly any neighbouring cell will pass on this very number set to its opposite vertices, etc.
Those Grünbaum-Coxeter polytopes, marked by this asterisk, are, like
dihedra, somehow degenerate: for there, the vertex count of
GC(x-P-o-...-o-Q-o-R-o-S-o)
equals the vertex count of its cells
e(x-P-o-...-o-Q-o-R-o),
and that vertex count in turn equals moreover the vertex count of the ridges
x-P-o-...-o-Q-o.
GC(x¯4¯o¯2n¯o)
(n>1)
*)
|
mod(e(. . .)) | 2 | n | n
--------------+---+---+--
mod( x . . ) | 2 | n | 2
--------------+---+---+--
mod(e(x4o .)) | 2 | 2 | n
|
GC(x¯2n¯o¯4¯o)
(n>1)
|
mod(e(. . .)) | n | 2 | 2
---------------+---+---+--
mod( x . . ) | 2 | n | 2
---------------+---+---+--
mod(e(x2no .)) | n | n | 2
|
|
GC(o4x4o)
|
mod(e(. . .)) | 2 | 2 | 1 1
--------------+---+---+----
mod( . x . ) | 2 | 2 | 1 1
--------------+---+---+----
mod(e(o4x .)) | 2 | 2 | 1 *
mod(e(. x4o)) | 2 | 2 | * 1
| | |
|
GC(x6o6o)
|
mod(e(. . .)) | 4 | 3 | 3
--------------+---+---+--
mod( x . . ) | 2 | 6 | 2
--------------+---+---+--
mod(e(x6o .)) | 3 | 3 | 4
| | |
|
GC(o6x6o)
|
mod(e(. . .)) | 3 | 2 | 1 1
--------------+---+---+----
mod( . x . ) | 2 | 3 | 1 1
--------------+---+---+----
mod(e(o6x .)) | 3 | 3 | 1 *
mod(e(. x6o)) | 3 | 3 | * 1
| | |
|
GC(x6o8o)
|
mod(e(. . .)) | 6 | 4 | 4
--------------+---+----+--
mod( x . . ) | 2 | 12 | 2
--------------+---+----+--
mod(e(x6o .)) | 3 | 3 | 8
|
GC(x8o6o)
|
mod(e(. . .)) | 8 | 3 | 3
--------------+---+----+--
mod( x . . ) | 2 | 12 | 2
--------------+---+----+--
mod(e(x8o .)) | 4 | 4 | 6
|
|
GC(x6o10o)
|
mod(e(. . .)) | 12 | 5 | 5
---------------+----+----+---
mod( x . . ) | 2 | 30 | 2
---------------+----+----+---
mod(e(x6o .)) | 3 | 3 | 20
|
GC(x10o6o)
|
mod(e(. . .)) | 20 | 3 | 3
---------------+----+----+---
mod( x . . ) | 2 | 30 | 2
---------------+----+----+---
mod(e(x10o .)) | 5 | 5 | 12
|
GC(x¯4¯o¯4¯o¯2n¯*a)
(n>1)
|
mod(e(. . . )) | n | 4 | 2 2
------------------+---+----+----
mod( x . . ) | 2 | 2n | 1 1
------------------+---+----+----
mod(e(x4o . )) | 2 | 2 | n *
mod(e(x . o2n*a)) | n | n | * 2
|
GC(o¯4¯x¯4¯o¯2n¯*a)
(n>1)
|
mod(e(. . . )) | 2 | 2 | 1 1
------------------+---+---+----
mod( . x . ) | 2 | 2 | 1 1
------------------+---+---+----
mod(e(o4x . )) | 2 | 2 | 1 *
mod(e(. x4o )) | 2 | 2 | * 1
|
|
GC(x6o4o6*a)
|
mod(e(. . . )) | 6 | 4 | 2 2
-----------------+---+----+----
mod( x . . ) | 2 | 12 | 1 1
-----------------+---+----+----
mod(e(x6o . )) | 3 | 3 | 4 *
mod(e(x . o6*a)) | 3 | 3 | * 4
| | |
|
GC(x6o4o8*a)
|
mod(e(. . . )) | 12 | 4 | 2 2
-----------------+----+----+----
mod( x . . ) | 2 | 24 | 1 1
-----------------+----+----+----
mod(e(x6o . )) | 3 | 3 | 8 *
mod(e(x . o8*a)) | 4 | 4 | * 6
| | |
|
GC(x6o4o10*a)
|
mod(e(. . . )) | 30 | 4 | 2 2
------------------+----+----+------
mod( x . . ) | 2 | 60 | 1 1
------------------+----+----+------
mod(e(x6o . )) | 3 | 3 | 20 *
mod(e(x . o10*a)) | 5 | 5 | * 12
| | |
GC(x3o4o3o)
*)
|
mod(e(. . . .)) | 3 ♦ 4 | 6 | 3
----------------+---+---+---+--
mod( x . . . ) | 2 | 6 | 3 | 3
----------------+---+---+---+--
mod( x3o . . ) | 3 | 3 | 6 | 2
----------------+---+---+---+--
mod(e(x3o4o .)) ♦ 3 | 6 | 4 | 3
| | |
GC(x4o3o4o)
*)
|
mod(e(. . . .)) | 4 ♦ 3 | 6 | 4
----------------+---+---+---+--
mod( x . . . ) | 2 | 6 | 4 | 4
----------------+---+---+---+--
mod( x4o . . ) | 4 | 4 | 6 | 2
----------------+---+---+---+--
mod(e(x4o3o .)) ♦ 4 | 6 | 3 | 4
| | |
GC(x4o3o5o)
*)
|
mod(e(. . . .)) | 4 ♦ 6 | 15 | 10
----------------+---+----+----+---
mod( x . . . ) | 2 | 12 | 5 | 5
----------------+---+----+----+---
mod( x4o . . ) | 4 | 4 | 15 | 2
----------------+---+----+----+---
mod(e(x4o3o .)) ♦ 4 | 6 | 3 | 10
|
GC(x5o3o4o)
|
mod(e(. . . .)) | 10 ♦ 3 | 6 | 4
----------------+----+----+----+--
mod( x . . . ) | 2 | 15 | 4 | 4
----------------+----+----+----+--
mod( x5o . . ) | 5 | 5 | 12 | 2
----------------+----+----+----+--
mod(e(x5o3o .)) ♦ 10 | 15 | 6 | 4
|
GC(x3o5o3o)
"11-cell"

|
mod(e(. . . .)) | 11 ♦ 10 | 15 | 6
----------------+----+----+----+---
mod( x . . . ) | 2 | 55 | 3 | 3
----------------+----+----+----+---
mod( x3o . . ) | 3 | 3 | 55 | 2
----------------+----+----+----+---
mod(e(x3o5o .)) ♦ 6 | 15 | 10 | 11
| | |
GC(x5o3o5o)
"57-cell"

|
mod(e(. . . .)) | 57 ♦ 6 | 15 | 10
----------------+----+-----+-----+---
mod( x . . . ) | 2 | 171 | 5 | 5
----------------+----+-----+-----+---
mod( x5o . . ) | 5 | 5 | 171 | 2
----------------+----+-----+-----+---
mod(e(x5o3o .)) ♦ 10 | 15 | 6 | 57
| | |
|
GC(x4o3o4o3*a)
|
mod(e(. . . . )) | 7 ♦ 12 | 12 12 | 4 6 3
-------------------+---+----+-------+------
mod( x . . . ) | 2 | 42 | 2 2 | 1 2 1
-------------------+---+----+-------+------
mod( x4o . . ) | 4 | 4 | 21 * | 1 1 0
mod( x . . o3*a ) | 3 | 3 | * 28 | 0 1 1
-------------------+---+----+-------+------
mod(e(x4o3o . )) ♦ 4 | 6 | 3 0 | 7 * *
mod(e(x4o . o3*a)) ♦ 6 | 12 | 3 4 | * 7 *
mod(e(x . o4o3*a)) ♦ 3 | 6 | 0 4 | * * 7
|
GC(x5o3o5o3*a)
(N so far unknown)
|
mod(e(. . . . )) | N ♦ 30 | 30 30 | 10 15 6
-------------------+----+-----+--------+--------
mod( x . . . ) | 2 | 15N | 2 2 | 1 2 1
-------------------+----+-----+--------+--------
mod( x5o . . ) | 5 | 5 | 6N * | 1 1 0
mod( x . . o3*a ) | 3 | 3 | * 10N | 0 1 1
-------------------+----+-----+--------+--------
mod(e(x5o3o . )) ♦ 10 | 15 | 6 0 | N * *
mod(e(x5o . o3*a)) ♦ 15 | 30 | 6 10 | * N *
mod(e(x . o5o3*a)) ♦ 6 | 15 | 0 10 | * * N
|
GC(x4o3o5o3*a)
(N so far unknown)
|
mod(e(. . . . )) | 2N ♦ 30 | 30 30 | 10 15 6
-------------------+----+-----+---------+---------
mod( x . . . ) | 2 | 30N | 2 2 | 1 2 1
-------------------+----+-----+---------+---------
mod( x4o . . ) | 4 | 4 | 15N * | 1 1 0
mod( x . . o3*a ) | 3 | 3 | * 20N | 0 1 1
-------------------+----+-----+---------+---------
mod(e(x4o3o . )) ♦ 4 | 6 | 3 0 | 5N * *
mod(e(x4o . o3*a)) ♦ 6 | 12 | 3 4 | * 5N *
mod(e(x . o5o3*a)) ♦ 6 | 15 | 0 10 | * * 2N
|
GC(x5o3o4o3*a)
(N so far unknown)
|
mod(e(. . . . )) | 5N ♦ 12 | 12 12 | 4 6 3
-------------------+----+-----+---------+---------
mod( x . . . ) | 2 | 30N | 2 2 | 1 2 1
-------------------+----+-----+---------+---------
mod( x5o . . ) | 5 | 5 | 12N * | 1 1 0
mod( x . . o3*a ) | 3 | 3 | * 20N | 0 1 1
-------------------+----+-----+---------+---------
mod(e(x5o3o . )) ♦ 10 | 15 | 6 0 | 2N * *
mod(e(x5o . o3*a)) ♦ 15 | 30 | 6 10 | * 2N *
mod(e(x . o4o3*a)) ♦ 3 | 6 | 0 4 | * * 5N
|
GC(x3o3o *b4o)
(partial a) by
B. Monson, E. Schulte
just adding
(ρ0ρ1ρ3)3=1
|
mod_a(e(. . . .)) | 8 ♦ 6 | 12 | 4 3
---------------------+---+----+----+----
mod_a( x . . . ) | 2 | 24 | 4 | 2 2
---------------------+---+----+----+----
mod_a( x3o . . ) | 3 | 3 | 32 | 1 1
---------------------+---+----+----+----
mod_a( x3o3o ) ♦ 4 | 6 | 4 | 8 *
mod_a(e(x3o . *b4o)) ♦ 3 | 6 | 4 | * 8
|
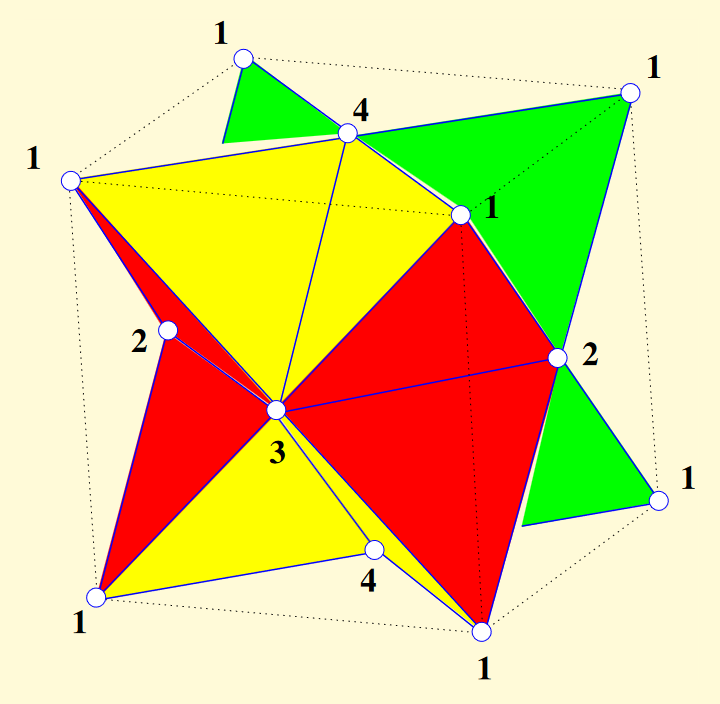
GC(x3o3o *b4o)
(partial b)
"Tomotope" by
B. Monson, D. Pellicer,
and G. Williams
|
mod_b(e(. . . .)) | 4 ♦ 6 | 12 | 4 3
---------------------+---+----+----+----
mod_b( x . . . ) | 2 | 12 | 4 | 2 2
---------------------+---+----+----+----
mod_b( x3o . . ) | 3 | 3 | 16 | 1 1
---------------------+---+----+----+----
mod_b( x3o3o ) ♦ 4 | 6 | 4 | 4 *
mod_b(e(x3o . *b4o)) ♦ 3 | 6 | 4 | * 4
|
GC(x3o3o4o3o)
*)
|
mod(e(. . . . .)) | 4 ♦ 12 | 48 | 48 | 12
------------------+---+----+----+----+---
mod( x . . . . ) | 2 | 24 ♦ 8 | 12 | 6
------------------+---+----+----+----+---
mod( x3o . . . ) | 3 | 3 | 64 | 3 | 3
------------------+---+----+----+----+---
mod( x3o3o . . ) ♦ 4 | 6 | 4 | 48 | 2
------------------+---+----+----+----+---
mod(e(x3o3o4o .)) ♦ 4 | 12 | 16 | 8 | 12
|
GC(x3o4o3o3o)
|
mod(e(. . . . .)) | 12 ♦ 8 | 16 | 12 | 4
------------------+----+----+----+----+--
mod( x . . . . ) | 2 | 48 ♦ 4 | 6 | 4
------------------+----+----+----+----+--
mod( x3o . . . ) | 3 | 3 | 64 | 3 | 3
------------------+----+----+----+----+--
mod( x3o4o . . ) ♦ 6 | 12 | 8 | 24 | 2
------------------+----+----+----+----+--
mod(e(x3o4o3o .)) ♦ 12 | 48 | 48 | 12 | 4
|
|
GC(o3x3o4o3o)
|
mod(e(. . . . .)) | 12 ♦ 8 | 4 12 | 6 6 | 3 1
------------------+----+----+-------+-------+----
mod( . x . . . ) | 2 | 48 ♦ 1 3 | 3 3 | 3 1
------------------+----+----+-------+-------+----
mod( o3x . . . ) | 3 | 3 | 16 * | 3 0 | 3 0
mod( . x3o . . ) | 3 | 3 | * 48 | 1 2 | 2 1
------------------+----+----+-------+-------+----
mod( o3x3o . . ) ♦ 6 | 12 | 4 4 | 12 * | 2 0
mod( . x3o4o . ) ♦ 6 | 12 | 0 8 | * 12 | 1 1
------------------+----+----+-------+-------+----
mod(e(o3x3o4o .)) ♦ 12 | 48 | 16 32 | 8 4 | 3 *
mod(e(. x3o4o3o)) ♦ 12 | 48 | 0 48 | 0 12 | * 1
| | |
GC(x4o3o3o4o)
*)
|
mod(e(. . . . .)) | 8 ♦ 4 | 12 | 16 | 8
------------------+---+----+----+----+--
mod( x . . . . ) | 2 | 16 ♦ 6 | 12 | 8
------------------+---+----+----+----+--
mod( x4o . . . ) | 4 | 4 | 24 | 4 | 4
------------------+---+----+----+----+--
mod( x4o3o . . ) ♦ 8 | 12 | 6 | 16 | 2
------------------+---+----+----+----+--
mod(e(x4o3o3o .)) ♦ 8 | 16 | 12 | 4 | 8
| | |
|
GC(o4o3x3o4o)
|
mod(e(. . . . .)) | 12 ♦ 8 | 8 8 | 2 8 2 | 2 2
------------------+----+----+-------+--------+----
mod( . . x . . ) | 2 | 48 ♦ 2 2 | 1 4 1 | 2 2
------------------+----+----+-------+--------+----
mod( . o3x . . ) | 3 | 3 | 32 * | 1 2 0 | 2 1
mod( . . x3o . ) | 3 | 3 | * 32 | 0 2 1 | 1 2
------------------+----+----+-------+--------+----
mod( o4o3x . . ) ♦ 6 | 12 | 8 0 | 4 * * | 2 0
mod( . o3x3o . ) ♦ 6 | 12 | 4 4 | * 16 * | 1 1
mod( . . x3o4o ) ♦ 6 | 12 | 0 8 | * * 4 | 0 2
------------------+----+----+-------+--------+----
mod(e(o4o3x3o .)) ♦ 12 | 48 | 32 16 | 4 8 0 | 2 *
mod(e(. o3x3o4o)) ♦ 12 | 48 | 16 32 | 0 8 4 | * 2
| | |
GC(x4o3o3o5o)
*)
|
mod(e(. . . . .)) | 8 ♦ 60 | 360 | 600 | 300
------------------+---+-----+-----+-----+----
mod( x . . . . ) | 2 | 240 ♦ 12 | 30 | 20
------------------+---+-----+-----+-----+----
mod( x4o . . . ) | 4 | 4 | 720 | 5 | 5
------------------+---+-----+-----+-----+----
mod( x4o3o . . ) ♦ 8 | 12 | 6 | 600 | 2
------------------+---+-----+-----+-----+----
mod(e(x4o3o3o .)) ♦ 8 | 16 | 12 | 4 | 300
|
GC(x5o3o3o4o)
|
mod(e(. . . . .)) | 300 ♦ 4 | 12 | 16 | 8
------------------+-----+-----+-----+-----+--
mod( x . . . . ) | 2 | 600 ♦ 6 | 12 | 8
------------------+-----+-----+-----+-----+--
mod( x5o . . . ) | 5 | 5 | 720 | 4 | 4
------------------+-----+-----+-----+-----+--
mod( x5o3o . . ) ♦ 20 | 30 | 12 | 240 | 2
------------------+-----+-----+-----+-----+--
mod(e(x5o3o3o .)) ♦ 300 | 600 | 360 | 60 | 8
|
GC(x5o3o3o5o)
(N so far unknown)
|
mod(e(. . . . .)) | N ♦ 60 | 360 | 600 | 300
------------------+-----+-----+-----+-----+----
mod( x . . . . ) | 2 | 30N ♦ 12 | 30 | 20
------------------+-----+-----+-----+-----+----
mod( x5o . . . ) | 5 | 5 | 72N | 5 | 5
------------------+-----+-----+-----+-----+----
mod( x5o3o . . ) ♦ 20 | 30 | 12 | 30N | 2
------------------+-----+-----+-----+-----+----
mod(e(x5o3o3o .)) ♦ 300 | 600 | 360 | 60 | N
| | |
GC(x4o3o3o3o4o)
*)
|
mod(e(. . . . . .)) | 16 ♦ 5 | 20 | 40 | 40 | 16
--------------------+----+----+----+----+----+---
mod( x . . . . . ) | 2 | 40 ♦ 8 | 24 | 32 | 16
--------------------+----+----+----+----+----+---
mod( x4o . . . . ) | 4 | 4 | 80 ♦ 6 | 12 | 8
--------------------+----+----+----+----+----+---
mod( x4o3o . . . ) ♦ 8 | 12 | 6 | 80 | 4 | 4
--------------------+----+----+----+----+----+---
mod( x4o3o3o . . ) ♦ 16 | 32 | 24 | 8 | 40 | 2
--------------------+----+----+----+----+----+---
mod(e(x4o3o3o3o .)) ♦ 16 | 40 | 40 | 20 | 5 | 16
| | |
|
GC(o4o3x3o3o4o)
|
mod(e(. . . . . .)) | 40 ♦ 12 | 12 24 | 3 24 16 | 6 16 2 | 4 2
--------------------+----+-----+---------+------------+----------+----
mod( . . x . . . ) | 2 | 240 | 2 4 | 1 8 4 | 4 8 1 | 4 2
--------------------+----+-----+---------+------------+----------+----
mod( . o3x . . . ) | 3 | 3 | 160 * | 1 4 0 | 4 4 0 | 4 1
mod( . . x3o . . ) | 3 | 3 | * 320 | 0 2 2 | 1 4 1 | 2 2
--------------------+----+-----+---------+------------+----------+----
mod( o4o3x . . . ) ♦ 6 | 12 | 8 0 | 20 * * | 4 0 0 | 4 0
mod( . o3x3o . . ) ♦ 6 | 12 | 4 4 | * 160 * | 1 2 0 | 2 1
mod( . . x3o3o . ) ♦ 4 | 6 | 0 4 | * * 160 | 0 2 1 | 1 2
--------------------+----+-----+---------+------------+----------+----
mod( o4o3x3o . . ) ♦ 24 | 96 | 64 32 | 8 16 0 | 10 * * | 2 0
mod( . o3x3o3o . ) ♦ 10 | 30 | 10 20 | 0 5 5 | * 64 * | 1 1
mod( . . x3o3o4o ) ♦ 8 | 24 | 0 32 | 0 0 16 | * * 10 | 0 2
--------------------+----+-----+---------+------------+----------+----
mod(e(o4o3x3o3o .)) ♦ 40 | 240 | 160 160 | 20 80 40 | 5 16 0 | 4 *
mod(e(. o3x3o3o4o)) ♦ 20 | 120 | 40 160 | 0 40 80 | 0 16 5 | * 4
| | |
For the regular ones the above list is complete, except that
in dimensions above 6 additionaly only the analogue of the single regular one of 6D does exist.
This is because that the pre-image structures within the parantheses might well be spherical, euclidean, or hyperbolic.
But the latter two cases subject to the additional demand that all its subelements must be spherical again.
Only then the vertex figures and the facets can be made elliptical by identifications across their centers
(provided those all have inversion symmetry).
For GC(x5o3o3o5o) so far only the incidence structure is known to me.
It well might be an infinite one none the same and therefore would then be omitted from this list again.
If this will come out to be true, then the famous 11-cell and 57-cell are the only finite Coxeter-Grünbaum polytopes which neither are
degenerate in the above mentioned sense (or dual to such) nor are isomorphic to usual regular polytopes of spherical space.
For the non-regular cases the above restrictions hold true again. (Especially the inversion symmetry of the vertex figure here is
a severe limitation.) The here listed ones are complete as long one considers
linear Dynkin diagrams for the pre-images only, and moreover the vertex figure polytope of those is uniform as well.
(Cases having uniform cells, but inversion symmetric vertex figure polytopes with different edge sizes, for either pre-images,
would exist in addition.)
Examples for either addition are given in several cases, but in no way are meant to be complete.
What is much more interesting however, is that truncation and rectification
is generally applicable to regular figures, even to mere abstract polytopes without any Wythoffian construction device.
Those being applied to the outstanding Coxeter and Grünbaum polytopes or the Monson-Pellicer-Williams tomotope run as follows:
trunc(mod(e(x3o5o3o)))
trops(mod( x . . . )) | 110 | 1 3 | 3 3 | 3 1
-----------------------+-----+--------+-------+------
trunc(mod( x . . . )) | 2 | 55 * | 3 0 | 3 0
verf( mod( x3o . . )) | 2 | * 165 | 1 2 | 2 1
-----------------------+-----+--------+-------+------
trunc(mod( x3o . . )) | 6 | 3 3 | 55 * | 2 0
verf( mod(e(x3o5o .))) | 5 | 0 5 | * 66 | 1 1
-----------------------+-----+--------+-------+------
trunc(mod(e(x3o5o .))) ♦ 30 | 15 30 | 10 6 | 11 *
verf( mod(e(x3o5o3o))) ♦ 10 | 0 15 | 0 6 | * 11
|
rect(mod(e(x3o5o3o)))
mids(mod( x . . . )) | 55 | 6 | 3 6 | 3 2
----------------------+----+-----+-------+------
verf(mod( x3o . . )) | 2 | 165 | 1 2 | 2 1
----------------------+----+-----+-------+------
rect(mod( x3o . . )) | 3 | 3 | 55 * | 2 0
verf(mod(e(x3o5o .))) | 5 | 5 | * 66 | 1 1
----------------------+----+-----+-------+------
rect(mod(e(x3o5o .))) ♦ 15 | 30 | 10 6 | 11 *
verf(mod(e(x3o5o3o))) ♦ 10 | 15 | 0 6 | * 11
|
trunc(mod(e(x5o3o5o)))
trops(mod( x . . . )) | 342 | 1 5 | 5 5 | 5 1
-----------------------+-----+---------+---------+------
trunc(mod( x . . . )) | 2 | 171 * | 5 0 | 5 0
verf( mod( x5o . . )) | 2 | * 855 | 1 2 | 2 1
-----------------------+-----+---------+---------+------
trunc(mod( x5o . . )) | 10 | 5 5 | 171 * | 2 0
verf( mod(e(x5o3o .))) | 3 | 0 3 | * 570 | 1 1
-----------------------+-----+---------+---------+------
trunc(mod(e(x5o3o .))) ♦ 30 | 15 30 | 6 10 | 57 *
verf( mod(e(x5o3o5o))) ♦ 6 | 0 15 | 0 10 | * 57
|
rect(mod(e(x5o3o5o)))
mids(mod( x . . . )) | 171 | 10 | 5 10 | 5 2
----------------------+-----+-----+---------+------
verf(mod( x5o . . )) | 2 | 855 | 1 2 | 2 1
----------------------+-----+-----+---------+------
rect(mod( x5o . . )) | 5 | 5 | 171 * | 2 0
verf(mod(e(x5o3o .))) | 3 | 3 | * 570 | 1 1
----------------------+-----+-----+---------+------
rect(mod(e(x5o3o .))) ♦ 15 | 30 | 6 10 | 57 *
verf(mod(e(x5o3o5o))) ♦ 6 | 15 | 0 10 | * 57
|
trunc(mod(e(x3o3o *b4o)))
trops(mod( x . . . )) | 24 | 1 4 | 4 2 2 | 2 2 1
--------------------------+----+-------+----------+------
trunc(mod( x . . . )) | 2 | 12 * | 4 0 0 | 2 2 0
verf( mod( x3o . . )) | 2 | * 48 | 1 1 1 | 1 1 1
--------------------------+----+-------+----------+------
trunc(mod( x3o . . )) | 6 | 3 3 | 16 * * | 1 1 0
verf( mod( x3o3o . )) | 3 | 0 3 | * 16 * | 1 0 1
verf( mod(e(x3o . *b4o))) | 4 | 0 4 | * * 12 | 0 1 1
--------------------------+----+-------+----------+------
trunc(mod( x3o3o . )) ♦ 12 | 6 12 | 4 4 0 | 4 * *
trunc(mod(e(x3o . *b4o))) ♦ 12 | 6 12 | 4 0 3 | * 4 *
verf( mod(e(x3o3o *b4o))) ♦ 6 | 0 12 | 0 4 3 | * * 4
|
rect(mod(e(x3o3o *b4o)))
mids(mod( x . . . )) | 12 | 8 | 4 4 4 | 2 2 2
-------------------------+----+----+----------+------
verf(mod( x3o . . )) | 2 | 48 | 1 1 1 | 1 1 1
-------------------------+----+----+----------+------
rect(mod( x3o . . )) | 3 | 3 | 16 * * | 1 1 0
verf(mod( x3o3o . )) | 3 | 3 | * 16 * | 1 0 1
verf(mod(e(x3o . *b4o))) | 4 | 4 | * * 12 | 0 1 1
-------------------------+----+----+----------+------
rect(mod( x3o3o . )) ♦ 6 | 12 | 4 4 0 | 4 * *
rect(mod(e(x3o . *b4o))) ♦ 6 | 12 | 4 0 3 | * 4 *
verf(mod(e(x3o3o *b4o))) ♦ 6 | 12 | 0 4 3 | * * 4
|
The construction of Coxeter-Moser polytopes (a.k.a. regular maps) (up)
Regular maps, as being defined by Coxeter and Moser, are mod-wrap identifications from euclidean tilings, which thus get
rolled up into a torus. They usually are denoted as {P,Q}(r,s).
The easiest example here is {4,4}(n,0).
In fact it is no different from the regular skew Petrie-Coxeter polyhedron {4,4|n},
which in turn is nothing but the sub-complex of all the squares of the {n}x{n} duoprism.
At the right the construction of {4,4}(8,0) from a chessboard subsection of
squat gets visualized. Note that the distortion only occurs when the torus remains within 3D,
whenever the bend would run into the 4th dimension, the same can be done without any distortion.
The general definition of {P,Q}(r,s) is possible whenever either P or Q is even.
For {P,Q}={2p,Q} one steps via face-edge-face the path (r,s) through the tiling, while
for {P,Q}={P,2q} one steps via vertex-edge-vertex the path (r,s) through the tiling,
until the identification of the modwrap takes place. Thus the repetition unit here always is some possibly scaled and/or rotated square layed on top of the tiling.
To that end for squat one defines 2 vectors X=(r,s) and
Y=(-s,r), with r ≥ s ≥ 0. Only when r=s or s=0
this regular map is reflexible.
For hexat and trat a similar
approach works as well. So the basis vectors for the index coordinates here are to be taken at an angle of π/3 or 60° instead.
Thus the repetition unit here always is some possibly scaled and/or rotated 60°-rhomb layed on top of the tiling.
For sure being cut original tiles can be reshuffled to the other, being identified side instead so that a more apealing fundamental patch occurs,
cf. the examples given below.
Clearly, only if {P,Q} was a
euclidean tiling, then the outcome will become a toroidal polytope.
For hyperbolic tilings shapes with even higher genus would result.
|
Maps of type {4,4}
|
|---|
|
{4,4}(1,0)
|
1 | 2 | 1
--+---+--
1 | 2 | 1
--+---+--
1 | 2 | 1
|
 © ©
|
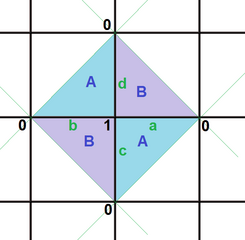
{4,4}(1,1)
|
2 | 4 | 2
--+---+--
2 | 4 | 2
--+---+--
2 | 4 | 2
|
 © ©
|
|
{4,4}(2,0)
|
4 | 4 | 4
--+---+--
2 | 8 | 2
--+---+--
4 | 4 | 4
|
 © ©
|
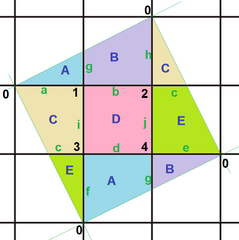
{4,4}(2,1)
|
5 | 4 | 4
--+----+--
2 | 10 | 2
--+----+--
4 | 4 | 5
|
 © ©
|
|
Maps of type {3,6}
|
|---|
|
{3,6}(1,0)
|
1 | 3 | 2
--+---+--
1 | 3 | 2
--+---+--
1 | 3 | 2
|
 © ©
|
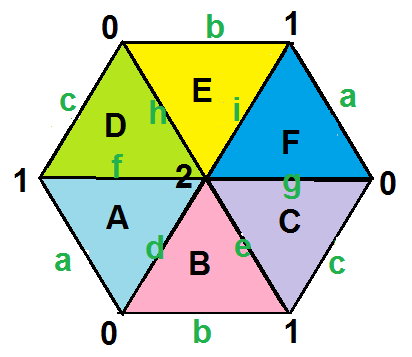
{3,6}(1,1)
|
3 | 6 | 6
--+---+--
2 | 9 | 2
--+---+--
3 | 3 | 6
|
 © ©
|
|
{3,6}(2,0)
|
4 | 6 | 6
--+----+--
2 | 12 | 2
--+----+--
3 | 3 | 8
|
 © ©
|
{3,6}(2,1)
|
7 | 6 | 6
--+----+---
2 | 21 | 2
--+----+---
3 | 3 | 14
|
 © ©
|
|
Maps of type {6,3}
|
|---|
|
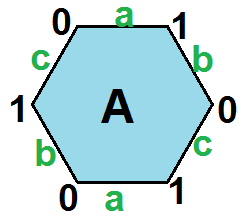
{6,3}(1,0)
|
2 | 3 | 1
--+---+--
2 | 3 | 1
--+---+--
2 | 3 | 1
|
 © ©
|
{6,3}(1,1)
|
6 | 3 | 3
--+---+--
2 | 9 | 2
--+---+--
6 | 6 | 3
|
 © ©
|
|
{6,3}(2,0)
|
8 | 3 | 3
--+----+--
2 | 12 | 2
--+----+--
6 | 6 | 4
|
 © ©
|
{6,3}(2,1)
|
14 | 3 | 3
---+----+--
2 | 21 | 2
---+----+--
6 | 6 | 7
|
 © ©
|
The same construction can be applied for sure with {4,3,...,3,4}(r,s,...,t,u) for a whole range of higher dimensional cases.
As well as to the only 2 exceptional cases {3,3,4,3}(r,s,t,u) and {3,4,3,3}(r,s,t,u).



 ©
©
 ©
©
 ©
©
 ©
©
 ©
©


.png)














